Advertisements
Advertisements
प्रश्न
The median of an equilateral triangle is increasing at the ratio of `2sqrt(3)` cm/s. Find the rate at which its side is increasing.
उत्तर
Let ‘a’ be the side of an equilateral triangle.
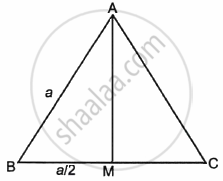
Medain AM = `sqrt(3)/2a`
Given `(d(AM))/(dt) = 2sqrt(3)` cm/s
`(d(AM))/(dt) = (d(sqrt(3)/2a))/(da) xx (da)/dt`
`2sqrt(3) = sqrt(3)/2 . (da)/dt`
`\implies (da)/dt` = 4 cm/s
APPEARS IN
संबंधित प्रश्न
A point source of light is hung 30 feet directly above a straight horizontal path on which a man of 6 feet in height is walking. How fast will the man’s shadow lengthen and how fast will the tip of shadow move when he is walking away from the light at the rate of 100 ft/min.
A stone is dropped into a quiet lake and waves move in circles at the speed of 5 cm/s. At the instant when the radius of the circular wave is 8 cm, how fast is the enclosed area increasing?
The length x of a rectangle is decreasing at the rate of 5 cm/minute and the width y is increasing at the rate of 4 cm/minute. When x = 8 cm and y = 6 cm, find the rates of change of (a) the perimeter, and (b) the area of the rectangle.
A balloon, which always remains spherical has a variable radius. Find the rate at which its volume is increasing with the radius when the later is 10 cm.
A ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2 cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall?
The total revenue in rupees received from the sale of x units of a product is given by R(x) = 13x2 + 26x + 15. Find the marginal revenue when x = 7.
The total revenue in rupees received from the sale of x units of a product is given by R(x) = 3x2 + 36x + 5. The marginal revenue, when x = 15 is ______.
Find the rate of change of the volume of a sphere with respect to its diameter ?
The total cost C (x) associated with the production of x units of an item is given by C (x) = 0.007x3 − 0.003x2 + 15x + 4000. Find the marginal cost when 17 units are produced ?
The radius of a spherical soap bubble is increasing at the rate of 0.2 cm/sec. Find the rate of increase of its surface area, when the radius is 7 cm.
The radius of an air bubble is increasing at the rate of 0.5 cm/sec. At what rate is the volume of the bubble increasing when the radius is 1 cm?
A man 2 metres high walks at a uniform speed of 5 km/hr away from a lamp-post 6 metres high. Find the rate at which the length of his shadow increases.
A man 160 cm tall, walks away from a source of light situated at the top of a pole 6 m high, at the rate of 1.1 m/sec. How fast is the length of his shadow increasing when he is 1 m away from the pole?
If y = 7x − x3 and x increases at the rate of 4 units per second, how fast is the slope of the curve changing when x = 2?
A particle moves along the curve y = x3. Find the points on the curve at which the y-coordinate changes three times more rapidly than the x-coordinate.
A particle moves along the curve y = (2/3)x3 + 1. Find the points on the curve at which the y-coordinate is changing twice as fast as the x-coordinate ?
Find the point on the curve y2 = 8x for which the abscissa and ordinate change at the same rate ?
The volume of a spherical balloon is increasing at the rate of 25 cm3/sec. Find the rate of change of its surface area at the instant when radius is 5 cm ?
The length x of a rectangle is decreasing at the rate of 5 cm/minute and the width y is increasing at the rate of 4 cm/minute. When x = 8 cm and y = 6 cm, find the rates of change of the area of the rectangle.
A cylindrical vessel of radius 0.5 m is filled with oil at the rate of 0.25 π m3/minute. The rate at which the surface of the oil is rising, is
The radius of a sphere is increasing at the rate of 0.2 cm/sec. The rate at which the volume of the sphere increase when radius is 15 cm, is
If the rate of change of area of a circle is equal to the rate of change of its diameter, then its radius is equal to
The diameter of a circle is increasing at the rate of 1 cm/sec. When its radius is π, the rate of increase of its area is
Evaluate: `int (x(1+x^2))/(1+x^4)dx`
A spherical ball of salt is dissolving in water in such a manner that the rate of decrease of the volume at any instant is proportional to the surface. Prove that the radius is decreasing at a constant rate
x and y are the sides of two squares such that y = x – x2. Find the rate of change of the area of second square with respect to the area of first square.
The radius of a cylinder is increasing at the rate of 3 m/s and its height is decreasing at the rate of 4 m/s. The rate of change of volume when the radius is 4 m and height is 6 m, is ____________.
The rate of change of volume of a sphere is equal to the rate of change of the radius than its radius equal to ____________.
A man 1.6 m tall walks at the rate of 0.3 m/sec away from a street light that is 4 m above the ground. At what rate is the tip of his shadow moving? At what rate is his shadow lengthening?
A spherical balloon is being inflated at the rate of 35 cc/min. The rate of increase in the surface area (in cm2/min.) of the balloon when its diameter is 14 cm, is ______.
