Advertisements
Advertisements
प्रश्न
A man 2 metres high walks at a uniform speed of 5 km/hr away from a lamp-post 6 metres high. Find the rate at which the length of his shadow increases.
उत्तर
Let AB be the lamp post. Suppose at any time t, the man CD be at a distance of x km from the lamp post and y m be the length of his shadow CE.
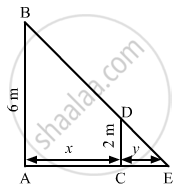
\[\text { Since triangles ABE and CDE are similar }, \]
\[\frac{AB}{CD} = \frac{AE}{CE}\]
\[ \Rightarrow \frac{6}{2} = \frac{x + y}{y}\]
\[ \Rightarrow 3y = x + y\]
\[ \Rightarrow x = 2y\]
\[ \Rightarrow \frac{dx}{dt} = 2\frac{dy}{dt}\]
\[ \Rightarrow \frac{dy}{dt} = \frac{1}{2}\frac{dx}{dt}\]
\[ \Rightarrow \frac{dy}{dt} = \frac{1}{2}\left( 5 \right) \left( \frac{dx}{dt} = 5 \right)\]
\[ \Rightarrow \frac{dy}{dt} = \frac{5}{2} km/hr\]
APPEARS IN
संबंधित प्रश्न
The rate of growth of bacteria is proportional to the number present. If, initially, there were
1000 bacteria and the number doubles in one hour, find the number of bacteria after 2½
hours.
[Take `sqrt2` = 1.414]
The volume of a cube is increasing at the rate of 8 cm3/s. How fast is the surface area increasing when the length of an edge is 12 cm?
An edge of a variable cube is increasing at the rate of 3 cm/s. How fast is the volume of the cube increasing when the edge is 10 cm long?
The radius of a circle is increasing at the rate of 0.7 cm/s. What is the rate of increase of its circumference?
The radius of an air bubble is increasing at the rate `1/2` cm/s. At what rate is the volume of the bubble increasing when the radius is 1 cm?
A balloon, which always remains spherical, has a variable diameter `3/2 (2x + 1)` Find the rate of change of its volume with respect to x.
The sum of the perimeter of a circle and square is k, where k is some constant. Prove that the sum of their areas is least when the side of square is double the radius of the circle.
The total cost C(x) associated with the production of x units of an item is given by C(x) = 0.005x3 – 0.02x2 + 30x + 5000. Find the marginal cost when 3 units are produced, whereby marginal cost we mean the instantaneous rate of change of total cost at any level of output.
Find the rate of change of the volume of a cone with respect to the radius of its base ?
Find the rate of change of the area of a circle with respect to its radius r when r = 5 cm
The total revenue received from the sale of x units of a product is given by R (x) = 13x2 + 26x + 15. Find the marginal revenue when x = 7 ?
An edge of a variable cube is increasing at the rate of 3 cm per second. How fast is the volume of the cube increasing when the edge is 10 cm long?
The side of a square is increasing at the rate of 0.2 cm/sec. Find the rate of increase of the perimeter of the square.
A balloon which always remains spherical, is being inflated by pumping in 900 cubic centimetres of gas per second. Find the rate at which the radius of the balloon is increasing when the radius is 15 cm.
A man 2 metres high walks at a uniform speed of 6 km/h away from a lamp-post 6 metres high. Find the rate at which the length of his shadow increases ?
The surface area of a spherical bubble is increasing at the rate of 2 cm2/s. When the radius of the bubble is 6 cm, at what rate is the volume of the bubble increasing?
If a particle moves in a straight line such that the distance travelled in time t is given by s = t3 − 6t2+ 9t + 8. Find the initial velocity of the particle ?
The amount of pollution content added in air in a city due to x diesel vehicles is given by P(x) = 0.005x3 + 0.02x2 + 30x. Find the marginal increase in pollution content when 3 diesel vehicles are added and write which value is indicated in the above questions ?
If \[V = \frac{4}{3}\pi r^3\] , at what rate in cubic units is V increasing when r = 10 and \[\frac{dr}{dt} = 0 . 01\] ? _________________
The radius of a sphere is changing at the rate of 0.1 cm/sec. The rate of change of its surface area when the radius is 200 cm is
A cone whose height is always equal to its diameter is increasing in volume at the rate of 40 cm3/sec. At what rate is the radius increasing when its circular base area is 1 m2?
The volume of a sphere is increasing at the rate of 4π cm3/sec. The rate of increase of the radius when the volume is 288 π cm3, is
If the rate of change of area of a circle is equal to the rate of change of its diameter, then its radius is equal to
In a sphere the rate of change of surface area is
A cylindrical tank of radius 10 m is being filled with wheat at the rate of 314 cubic metre per hour. Then the depth of the wheat is increasing at the rate of
Evaluate: `int (x(1+x^2))/(1+x^4)dx`
A spherical ball of salt is dissolving in water in such a manner that the rate of decrease of the volume at any instant is proportional to the surface. Prove that the radius is decreasing at a constant rate
Two men A and B start with velocities v at the same time from the junction of two roads inclined at 45° to each other. If they travel by different roads, find the rate at which they are being seperated.
The volume of a cube increases at a constant rate. Prove that the increase in its surface area varies inversely as the length of the side
x and y are the sides of two squares such that y = x – x2. Find the rate of change of the area of second square with respect to the area of first square.
The instantaneous rate of change at t = 1 for the function f (t) = te-t + 9 is ____________.
What is the rate of change of the area of a circle with respect to its radius when, r = 3 cm
If equal sides of an isosceles triangle with fixed base 10 cm are increasing at the rate of 4 cm/sec, how fast is the area of triangle increasing at an instant when all sides become equal?
Given that `1/y + 1/x = 1/12` and y decreases at a rate of 1 cms–1, find the rate of change of x when x = 5 cm and y = 1 cm.
