Advertisements
Advertisements
प्रश्न
A man 2 metres high walks at a uniform speed of 5 km/hr away from a lamp-post 6 metres high. Find the rate at which the length of his shadow increases.
उत्तर
Let AB be the lamp post. Suppose at any time t, the man CD be at a distance of x km from the lamp post and y m be the length of his shadow CE.
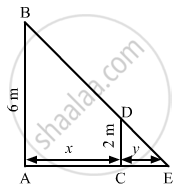
\[\text { Since triangles ABE and CDE are similar }, \]
\[\frac{AB}{CD} = \frac{AE}{CE}\]
\[ \Rightarrow \frac{6}{2} = \frac{x + y}{y}\]
\[ \Rightarrow 3y = x + y\]
\[ \Rightarrow x = 2y\]
\[ \Rightarrow \frac{dx}{dt} = 2\frac{dy}{dt}\]
\[ \Rightarrow \frac{dy}{dt} = \frac{1}{2}\frac{dx}{dt}\]
\[ \Rightarrow \frac{dy}{dt} = \frac{1}{2}\left( 5 \right) \left( \frac{dx}{dt} = 5 \right)\]
\[ \Rightarrow \frac{dy}{dt} = \frac{5}{2} km/hr\]
APPEARS IN
संबंधित प्रश्न
The total cost C(x) in rupees associated with the production of x units of an item is given by C(x) = 0.007x3 – 0.003x2 + 15x + 4000. Find the marginal cost when 17 units are produced
The total revenue in rupees received from the sale of x units of a product is given by R(x) = 13x2 + 26x + 15. Find the marginal revenue when x = 7.
The two equal sides of an isosceles triangle with fixed base b are decreasing at the rate of 3 cm per second. How fast is the area decreasing when the two equal sides are equal to the base?
The volume of a sphere is increasing at the rate of 8 cm3/s. Find the rate at which its surface area is increasing when the radius of the sphere is 12 cm.
The volume of a sphere is increasing at the rate of 3 cubic centimeter per second. Find the rate of increase of its surface area, when the radius is 2 cm
Find the rate of change of the volume of a sphere with respect to its diameter ?
The total cost C (x) associated with the production of x units of an item is given by C (x) = 0.007x3 − 0.003x2 + 15x + 4000. Find the marginal cost when 17 units are produced ?
The side of a square sheet is increasing at the rate of 4 cm per minute. At what rate is the area increasing when the side is 8 cm long?
The radius of a circle is increasing at the rate of 0.7 cm/sec. What is the rate of increase of its circumference?
A balloon in the form of a right circular cone surmounted by a hemisphere, having a diameter equal to the height of the cone, is being inflated. How fast is its volume changing with respect to its total height h, when h = 9 cm.
A kite is 120 m high and 130 m of string is out. If the kite is moving away horizontally at the rate of 52 m/sec, find the rate at which the string is being paid out.
Find the point on the curve y2 = 8x for which the abscissa and ordinate change at the same rate ?
The radius of a sphere is changing at the rate of 0.1 cm/sec. The rate of change of its surface area when the radius is 200 cm is
The distance moved by the particle in time t is given by x = t3 − 12t2 + 6t + 8. At the instant when its acceleration is zero, the velocity is
The radius of the base of a cone is increasing at the rate of 3 cm/minute and the altitude is decreasing at the rate of 4 cm/minute. The rate of change of lateral surface when the radius = 7 cm and altitude 24 cm is
The radius of a sphere is increasing at the rate of 0.2 cm/sec. The rate at which the volume of the sphere increase when radius is 15 cm, is
The volume of a sphere is increasing at 3 cm3/sec. The rate at which the radius increases when radius is 2 cm, is
If the rate of change of volume of a sphere is equal to the rate of change of its radius, then its radius is equal to
If the rate of change of area of a circle is equal to the rate of change of its diameter, then its radius is equal to
If s = t3 − 4t2 + 5 describes the motion of a particle, then its velocity when the acceleration vanishes, is
The radius of a circular plate is increasing at the rate of 0.01 cm/sec. The rate of increase of its area when the radius is 12 cm, is
The diameter of a circle is increasing at the rate of 1 cm/sec. When its radius is π, the rate of increase of its area is
A man of height 6 ft walks at a uniform speed of 9 ft/sec from a lamp fixed at 15 ft height. The length of his shadow is increasing at the rate of
A ladder 13 m long is leaning against a vertical wall. The bottom of the ladder is dragged away from the wall along the ground at the rate of 2 cm/sec. How fast is the height on the wall decreasing when the foot of the ladder is 5 m away from the wall.
If the area of a circle increases at a uniform rate, then prove that perimeter varies inversely as the radius
A swimming pool is to be drained for cleaning. If L represents the number of litres of water in the pool t seconds after the pool has been plugged off to drain and L = 200 (10 – t)2. How fast is the water running out at the end of 5 seconds? What is the average rate at which the water flows out during the first 5 seconds?
The sides of an equilateral triangle are increasing at the rate of 2 cm/sec. The rate at which the area increases, when side is 10 cm is ______.
Total revenue in rupees received from the sale of x units of a product is given by R(x)= 3x2+ 36x + 5. The marginal revenue, when x = 15 is ____________.
The rate of change of volume of a sphere is equal to the rate of change of the radius than its radius equal to ____________.
A cylindrical tank of radius 10 feet is being filled with wheat at the rate of 3/4 cubic feet per minute. The then depth of the wheat is increasing at the rate of
A spherical balloon is being inflated at the rate of 35 cc/min. The rate of increase in the surface area (in cm2/min.) of the balloon when its diameter is 14 cm, is ______.
An edge of a variable cube is increasing at the rate of 10 cm/sec. How fast will the volume of the cube increase if the edge is 5 cm long?
A kite is being pulled down by a string that goes through a ring on the ground 8 meters away from the person pulling it. If the string is pulled in at 1 meter per second, how fast is the kite coming down when it is 15 meters high?
