Question

A balloon in the form of a right circular cone surmounted by a hemisphere, having a diameter equal to the height of the cone, is being inflated. How fast is its volume changing with respect to its total height h, when h = 9 cm.

Answer 1

\[\text { Let r be the radius of the hemisphere, h be the height and V be the volume of the cone  }.\]

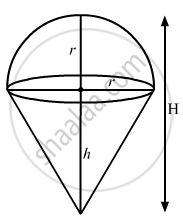
Then,

\[H = h + r \]

\[ \Rightarrow H = 3r \left[ \because h = 2r \right]\]

\[ \Rightarrow \frac{dH}{dt} = 3\frac{dr}{dt}\]

\[\text { When } H =  \text{9    cm}, r = \text{3 cm}\]

\[\text { Volume } =\frac{1}{3} \pi r^2 h+\frac{2}{3}\pi r^3 \]

\[\text {Substituting h }=2r\]

\[\Rightarrow V=\frac{2}{3}\pi r^3 +\frac{2}{3}\pi r^3 \]

\[\Rightarrow V=\frac{4}{3}\pi r^3 \]

\[\Rightarrow\frac{dV}{dt}=4\pi r^2 \frac{dr}{dt}\]

\[\Rightarrow\frac{dV}{dt}=\frac{4\pi r^2}{3}\frac{dH}{dt}\]

\[\Rightarrow\frac{dV}{dH}=\frac{4\pi \left( 3 \right)^2}{3}\]

\[\Rightarrow\frac{dV}{dH} {=\text{12} \pi  cm}^3 /sec\]