Advertisements
Advertisements
प्रश्न
An edge of a variable cube is increasing at the rate of 10 cm/sec. How fast will the volume of the cube increase if the edge is 5 cm long?
विकल्प
75 cm3/sec
750 cm3/sec
7500 cm3/sec
1250 cm3/sec
उत्तर
750 cm3/sec
Explanation:
Let x be edge of cube.
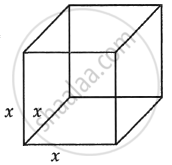
Given `dx/dt` = 10 cm/sec
Volume of the cube V = x3
∴ `(dV)/dt = 3x^2 dx/dt`
When x = 5 cm
`(dV)/dt` = 3 × 52 × 10
= 750 cm3/sec.
APPEARS IN
संबंधित प्रश्न
Find the rate of change of the area of a circle with respect to its radius r when r = 3 cm.
An edge of a variable cube is increasing at the rate of 3 cm/s. How fast is the volume of the cube increasing when the edge is 10 cm long?
The radius of a circle is increasing at the rate of 0.7 cm/s. What is the rate of increase of its circumference?
A particle moves along the curve 6y = x3 +2. Find the points on the curve at which the y-coordinate is changing 8 times as fast as the x-coordinate.
The radius of an air bubble is increasing at the rate `1/2` cm/s. At what rate is the volume of the bubble increasing when the radius is 1 cm?
Sand is pouring from a pipe at the rate of 12 cm3/s. The falling sand forms a cone on the ground in such a way that the height of the cone is always one-sixth of the radius of the base. How fast is the height of the sand cone increasing when the height is 4 cm?
The total revenue in rupees received from the sale of x units of a product is given by R(x) = 13x2 + 26x + 15. Find the marginal revenue when x = 7.
Find the rate of change of the total surface area of a cylinder of radius r and height h, when the radius varies?
Find the rate of change of the area of a circular disc with respect to its circumference when the radius is 3 cm ?
A balloon which always remains spherical, is being inflated by pumping in 900 cubic centimetres of gas per second. Find the rate at which the radius of the balloon is increasing when the radius is 15 cm.
If y = 7x − x3 and x increases at the rate of 4 units per second, how fast is the slope of the curve changing when x = 2?
Find an angle θ which increases twice as fast as its cosine ?
A man 2 metres high walks at a uniform speed of 6 km/h away from a lamp-post 6 metres high. Find the rate at which the length of his shadow increases ?
The radius of a cylinder is increasing at the rate 2 cm/sec. and its altitude is decreasing at the rate of 3 cm/sec. Find the rate of change of volume when radius is 3 cm and altitude 5 cm.
A kite is 120 m high and 130 m of string is out. If the kite is moving away horizontally at the rate of 52 m/sec, find the rate at which the string is being paid out.
The length x of a rectangle is decreasing at the rate of 5 cm/minute and the width y is increasing at the rate of 4 cm/minute. When x = 8 cm and y = 6 cm, find the rates of change of the area of the rectangle.
The amount of pollution content added in air in a city due to x diesel vehicles is given by P(x) = 0.005x3 + 0.02x2 + 30x. Find the marginal increase in pollution content when 3 diesel vehicles are added and write which value is indicated in the above questions ?
A cylindrical vessel of radius 0.5 m is filled with oil at the rate of 0.25 π m3/minute. The rate at which the surface of the oil is rising, is
The distance moved by the particle in time t is given by x = t3 − 12t2 + 6t + 8. At the instant when its acceleration is zero, the velocity is
In a sphere the rate of change of surface area is
A ladder 13 m long is leaning against a vertical wall. The bottom of the ladder is dragged away from the wall along the ground at the rate of 2 cm/sec. How fast is the height on the wall decreasing when the foot of the ladder is 5 m away from the wall.
Water is dripping out at a steady rate of 1 cu cm/sec through a tiny hole at the vertex of the conical vessel, whose axis is vertical. When the slant height of water in the vessel is 4 cm, find the rate of decrease of slant height, where the vertical angle of the conical vessel is `pi/6`
If the area of a circle increases at a uniform rate, then prove that perimeter varies inversely as the radius
A swimming pool is to be drained for cleaning. If L represents the number of litres of water in the pool t seconds after the pool has been plugged off to drain and L = 200 (10 – t)2. How fast is the water running out at the end of 5 seconds? What is the average rate at which the water flows out during the first 5 seconds?
The rate of change of volume of a sphere is equal to the rate of change of the radius than its radius equal to ____________.
The radius of a circle is increasing uniformly at the rate of 3 cm per second. Find the rate at which the area of the circle is increasing when the radius is 10 cm.
If equal sides of an isosceles triangle with fixed base 10 cm are increasing at the rate of 4 cm/sec, how fast is the area of triangle increasing at an instant when all sides become equal?
