Advertisements
Advertisements
Question
An edge of a variable cube is increasing at the rate of 10 cm/sec. How fast will the volume of the cube increase if the edge is 5 cm long?
Options
75 cm3/sec
750 cm3/sec
7500 cm3/sec
1250 cm3/sec
Solution
750 cm3/sec
Explanation:
Let x be edge of cube.
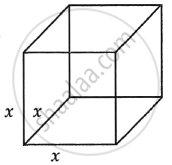
Given `dx/dt` = 10 cm/sec
Volume of the cube V = x3
∴ `(dV)/dt = 3x^2 dx/dt`
When x = 5 cm
`(dV)/dt` = 3 × 52 × 10
= 750 cm3/sec.
APPEARS IN
RELATED QUESTIONS
Find the rate of change of the area of a circle with respect to its radius r when r = 3 cm.
An edge of a variable cube is increasing at the rate of 3 cm/s. How fast is the volume of the cube increasing when the edge is 10 cm long?
The length x of a rectangle is decreasing at the rate of 5 cm/minute and the width y is increasing at the rate of 4 cm/minute. When x = 8 cm and y = 6 cm, find the rates of change of (a) the perimeter, and (b) the area of the rectangle.
Sand is pouring from a pipe at the rate of 12 cm3/s. The falling sand forms a cone on the ground in such a way that the height of the cone is always one-sixth of the radius of the base. How fast is the height of the sand cone increasing when the height is 4 cm?
The total revenue in rupees received from the sale of x units of a product is given by R(x) = 3x2 + 36x + 5. The marginal revenue, when x = 15 is ______.
The two equal sides of an isosceles triangle with fixed base b are decreasing at the rate of 3 cm per second. How fast is the area decreasing when the two equal sides are equal to the base?
The sum of the perimeter of a circle and square is k, where k is some constant. Prove that the sum of their areas is least when the side of square is double the radius of the circle.
The volume of a sphere is increasing at the rate of 8 cm3/s. Find the rate at which its surface area is increasing when the radius of the sphere is 12 cm.
An edge of a variable cube is increasing at the rate of 3 cm per second. How fast is the volume of the cube increasing when the edge is 10 cm long?
The radius of a spherical soap bubble is increasing at the rate of 0.2 cm/sec. Find the rate of increase of its surface area, when the radius is 7 cm.
A man 180 cm tall walks at a rate of 2 m/sec. away, from a source of light that is 9 m above the ground. How fast is the length of his shadow increasing when he is 3 m away from the base of light?
Sand is being poured onto a conical pile at the constant rate of 50 cm3/ minute such that the height of the cone is always one half of the radius of its base. How fast is the height of the pile increasing when the sand is 5 cm deep ?
The sides of an equilateral triangle are increasing at the rate of 2 cm/sec. How far is the area increasing when the side is 10 cms?
The radius of a circle is increasing at the rate of 0.5 cm/sec. Find the rate of increase of its circumference ?
The amount of pollution content added in air in a city due to x diesel vehicles is given by P(x) = 0.005x3 + 0.02x2 + 30x. Find the marginal increase in pollution content when 3 diesel vehicles are added and write which value is indicated in the above questions ?
For what values of x is the rate of increase of x3 − 5x2 + 5x + 8 is twice the rate of increase of x ?
Each side of an equilateral triangle is increasing at the rate of 8 cm/hr. The rate of increase of its area when side is 2 cm, is
If s = t3 − 4t2 + 5 describes the motion of a particle, then its velocity when the acceleration vanishes, is
The equation of motion of a particle is s = 2t2 + sin 2t, where s is in metres and t is in seconds. The velocity of the particle when its acceleration is 2 m/sec2, is
In a sphere the rate of change of volume is
A man, 2m tall, walks at the rate of `1 2/3` m/s towards a street light which is `5 1/3`m above the ground. At what rate is the tip of his shadow moving? At what rate is the length of the shadow changing when he is `3 1/3`m from the base of the light?
The volume of a cube increases at a constant rate. Prove that the increase in its surface area varies inversely as the length of the side
The radius of a cylinder is increasing at the rate of 3 m/s and its height is decreasing at the rate of 4 m/s. The rate of change of volume when the radius is 4 m and height is 6 m, is ____________.
Total revenue in rupees received from the sale of x units of a product is given by R(x)= 3x2+ 36x + 5. The marginal revenue, when x = 15 is ____________.
If the rate of change of the area of the circle is equal to the rate of change of its diameter then its radius is equal to ____________.
The median of an equilateral triangle is increasing at the ratio of `2sqrt(3)` cm/s. Find the rate at which its side is increasing.
