Advertisements
Advertisements
Question
The two equal sides of an isosceles triangle with fixed base b are decreasing at the rate of 3 cm per second. How fast is the area decreasing when the two equal sides are equal to the base?
Solution
Let us take either of the equal side AB and AC be x
⇒ `dx/dt = -3` cm/sec.
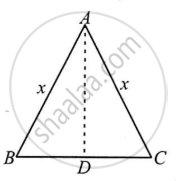
If A is the corresponding area of ΔABC
`A = 1/2` base × height = `1/2 b sqrt (AB^2 - BD^2)`
`= b/2 sqrt (x^2 - (b/2)^2)`
`= b/4 sqrt (4x^2 - b^2)`
`(dA)/dt = b/4 xx 1/2 xx (8x)/ sqrt (4x^2 - b^2) dx/dt`
`= (bx)/ sqrt (4x^2 - b^2) dx/dt`
`((dA)/dt)_(x = b) = ((b xxb)/ sqrt (4b^2 - b^2)) (-3)`
`= - sqrt(3b)`
Area is decreasing at the rate of `b sqrt3` cm2 sec
APPEARS IN
RELATED QUESTIONS
A point source of light is hung 30 feet directly above a straight horizontal path on which a man of 6 feet in height is walking. How fast will the man’s shadow lengthen and how fast will the tip of shadow move when he is walking away from the light at the rate of 100 ft/min.
The rate of growth of bacteria is proportional to the number present. If, initially, there were
1000 bacteria and the number doubles in one hour, find the number of bacteria after 2½
hours.
[Take `sqrt2` = 1.414]
The volume of a cube is increasing at the rate of 8 cm3/s. How fast is the surface area increasing when the length of an edge is 12 cm?
The radius of a circle is increasing at the rate of 0.7 cm/s. What is the rate of increase of its circumference?
Sand is pouring from a pipe at the rate of 12 cm3/s. The falling sand forms a cone on the ground in such a way that the height of the cone is always one-sixth of the radius of the base. How fast is the height of the sand cone increasing when the height is 4 cm?
The total revenue in rupees received from the sale of x units of a product is given by R(x) = 13x2 + 26x + 15. Find the marginal revenue when x = 7.
The volume of a sphere is increasing at the rate of 3 cubic centimeter per second. Find the rate of increase of its surface area, when the radius is 2 cm
Find the rate of change of the total surface area of a cylinder of radius r and height h, when the radius varies?
The radius of a circle is increasing at the rate of 0.7 cm/sec. What is the rate of increase of its circumference?
A balloon which always remains spherical, is being inflated by pumping in 900 cubic centimetres of gas per second. Find the rate at which the radius of the balloon is increasing when the radius is 15 cm.
The radius of an air bubble is increasing at the rate of 0.5 cm/sec. At what rate is the volume of the bubble increasing when the radius is 1 cm?
A particle moves along the curve y = x2 + 2x. At what point(s) on the curve are the x and y coordinates of the particle changing at the same rate?
Find an angle θ whose rate of increase twice is twice the rate of decrease of its cosine ?
A balloon in the form of a right circular cone surmounted by a hemisphere, having a diameter equal to the height of the cone, is being inflated. How fast is its volume changing with respect to its total height h, when h = 9 cm.
Sand is being poured onto a conical pile at the constant rate of 50 cm3/ minute such that the height of the cone is always one half of the radius of its base. How fast is the height of the pile increasing when the sand is 5 cm deep ?
Find the point on the curve y2 = 8x for which the abscissa and ordinate change at the same rate ?
The volume of a spherical balloon is increasing at the rate of 25 cm3/sec. Find the rate of change of its surface area at the instant when radius is 5 cm ?
The length x of a rectangle is decreasing at the rate of 5 cm/minute and the width y is increasing at the rate of 4 cm/minute. When x = 8 cm and y = 6 cm, find the rates of change of the perimeter.
The side of a square is increasing at the rate of 0.1 cm/sec. Find the rate of increase of its perimeter ?
Find the surface area of a sphere when its volume is changing at the same rate as its radius ?
If the rate of change of volume of a sphere is equal to the rate of change of its radius, find the radius of the sphere ?
The amount of pollution content added in air in a city due to x diesel vehicles is given by P(x) = 0.005x3 + 0.02x2 + 30x. Find the marginal increase in pollution content when 3 diesel vehicles are added and write which value is indicated in the above questions ?
A ladder, 5 metre long, standing on a horizontal floor, leans against a vertical wall. If the top of the ladder slides down wards at the rate of 10 cm/sec, then find the rate at which the angle between the floor and ladder is decreasing when lower end of ladder is 2 metres from the wall ?
Side of an equilateral triangle expands at the rate of 2 cm/sec. The rate of increase of its area when each side is 10 cm is
The volume of a sphere is increasing at 3 cm3/sec. The rate at which the radius increases when radius is 2 cm, is
Each side of an equilateral triangle is increasing at the rate of 8 cm/hr. The rate of increase of its area when side is 2 cm, is
If s = t3 − 4t2 + 5 describes the motion of a particle, then its velocity when the acceleration vanishes, is
The rate of change of volume of a sphere with respect to its surface area, when the radius is 2 cm, is ______.
A spherical ball of salt is dissolving in water in such a manner that the rate of decrease of the volume at any instant is proportional to the surface. Prove that the radius is decreasing at a constant rate
A kite is moving horizontally at a height of 151.5 meters. If the speed of kite is 10 m/s, how fast is the string being let out; when the kite is 250 m away from the boy who is flying the kite? The height of boy is 1.5 m.
A man, 2m tall, walks at the rate of `1 2/3` m/s towards a street light which is `5 1/3`m above the ground. At what rate is the tip of his shadow moving? At what rate is the length of the shadow changing when he is `3 1/3`m from the base of the light?
Total revenue in rupees received from the sale of x units of a product is given by R(x)= 3x2+ 36x + 5. The marginal revenue, when x = 15 is ____________.
If the rate of change of volume of a sphere is equal to the rate of change of its radius then the surface area of a sphere is ____________.
The radius of a circle is increasing uniformly at the rate of 3 cm per second. Find the rate at which the area of the circle is increasing when the radius is 10 cm.
A cylindrical tank of radius 10 feet is being filled with wheat at the rate of 3/4 cubic feet per minute. The then depth of the wheat is increasing at the rate of
If the circumference of circle is increasing at the constant rate, prove that rate of change of area of circle is directly proportional to its radius.
