Advertisements
Advertisements
प्रश्न
A ladder, 5 meter long, standing on a horizontal floor, leans against a vertical wall. If the top of the ladder slides downwards at the rate of 10 cm/sec, then the rate at which the angle between the floor and the ladder is decreasing when lower end of ladder is 2 metres from the wall is ______.
पर्याय
1/10` radian/sec
1/20 radian/sec
20 radian/sec
10 radian/sec
उत्तर
A ladder, 5 meter long, standing on a horizontal floor, leans against a vertical wall. If the top of the ladder slides downwards at the rate of 10 cm/sec, then the rate at which the angle between the floor and the ladder is decreasing when lower end of ladder is 2 metres from the wall is 1/20 radian/sec.
Explanation: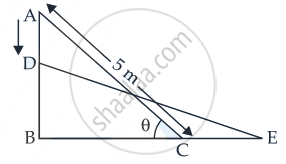
Length of ladder = 5 m
Let AB = y m and BC = x m
∴ In right ΔABC,
AB2 + BC2 = AC2
⇒ x2 + y2 = (5)2
⇒ x2 + y2 = 25
Differentiating both sides w.r.t x, we have
`2x * "dx"/"dt" + 2y * "dy"/"dt"` = 0
⇒ `x "dx"/"dt" + y * "dy"/"dt"` = 0
⇒ `2 * "dx"/"dt" + y xx (-0.1)` = 0 ....[∵ x = 2m]
⇒ `2 * "dx"/"dt" + sqrt(25 - x^2) xx (-0.1)` = 0
⇒ `2 * "dx"/"dt" + sqrt(25 - 4) xx (-0.1)` = 0
⇒ `2 * "dx"/"dt" - sqrt(21)/10` = 0
⇒ `"dx"/"dt" = sqrt(21)/20`
Now cos θ = `"BC"/"AC"` ....(θ is in radian)
⇒ cos θ = `x/5`
Differentiating both sides w.r.t. t, we get
`"d"/"dt" cos theta = 1/5 * "dx"/"dt"`
⇒ `- sin theta ("d"theta)/"dt" = 1/5 * sqrt(21)/20`
⇒ `("d"theta)/"dt" = sqrt(21)/100 xx (- 1/sin theta)`
= `sqrt(21)/100 xx -(1/("AB"/"AC"))`
= `- sqrt(21)/100 xx "AC"/"AB"`
= `- sqrt(21)/100 xx 5/sqrt(21)`
= `- 1/20` radian/sec
[(–) sign shows the decrease of change of angle]
Hence, the required rate = `1/20` radian/sec
APPEARS IN
संबंधित प्रश्न
The rate of growth of bacteria is proportional to the number present. If, initially, there were
1000 bacteria and the number doubles in one hour, find the number of bacteria after 2½
hours.
[Take `sqrt2` = 1.414]
The volume of a cube is increasing at the rate of 8 cm3/s. How fast is the surface area increasing when the length of an edge is 12 cm?
The radius of a circle is increasing at the rate of 0.7 cm/s. What is the rate of increase of its circumference?
A balloon, which always remains spherical, has a variable diameter `3/2 (2x + 1)` Find the rate of change of its volume with respect to x.
The rate of change of the area of a circle with respect to its radius r at r = 6 cm is ______.
The sum of the perimeter of a circle and square is k, where k is some constant. Prove that the sum of their areas is least when the side of square is double the radius of the circle.
Find the rate of change of the total surface area of a cylinder of radius r and height h, when the radius varies?
Find the rate of change of the volume of a cone with respect to the radius of its base ?
Find the rate of change of the area of a circle with respect to its radius r when r = 5 cm
Find the rate of change of the volume of a ball with respect to its radius r. How fast is the volume changing with respect to the radius when the radius is 2 cm?
The total cost C (x) associated with the production of x units of an item is given by C (x) = 0.007x3 − 0.003x2 + 15x + 4000. Find the marginal cost when 17 units are produced ?
An edge of a variable cube is increasing at the rate of 3 cm per second. How fast is the volume of the cube increasing when the edge is 10 cm long?
A balloon which always remains spherical, is being inflated by pumping in 900 cubic centimetres of gas per second. Find the rate at which the radius of the balloon is increasing when the radius is 15 cm.
A particle moves along the curve y = x3. Find the points on the curve at which the y-coordinate changes three times more rapidly than the x-coordinate.
Find an angle θ which increases twice as fast as its cosine ?
A man 2 metres high walks at a uniform speed of 6 km/h away from a lamp-post 6 metres high. Find the rate at which the length of his shadow increases ?
Sand is being poured onto a conical pile at the constant rate of 50 cm3/ minute such that the height of the cone is always one half of the radius of its base. How fast is the height of the pile increasing when the sand is 5 cm deep ?
The volume of a spherical balloon is increasing at the rate of 25 cm3/sec. Find the rate of change of its surface area at the instant when radius is 5 cm ?
A circular disc of radius 3 cm is being heated. Due to expansion, its radius increases at the rate of 0.05 cm/sec. Find the rate at which its area is increasing when radius is 3.2 cm.
The radius of a circle is increasing at the rate of 0.5 cm/sec. Find the rate of increase of its circumference ?
The amount of pollution content added in air in a city due to x diesel vehicles is given by P(x) = 0.005x3 + 0.02x2 + 30x. Find the marginal increase in pollution content when 3 diesel vehicles are added and write which value is indicated in the above questions ?
A ladder, 5 metre long, standing on a horizontal floor, leans against a vertical wall. If the top of the ladder slides down wards at the rate of 10 cm/sec, then find the rate at which the angle between the floor and ladder is decreasing when lower end of ladder is 2 metres from the wall ?
The radius of a sphere is increasing at the rate of 0.2 cm/sec. The rate at which the volume of the sphere increase when radius is 15 cm, is
In a sphere the rate of change of volume is
For the curve y = 5x – 2x3, if x increases at the rate of 2 units/sec, then how fast is the slope of curve changing when x = 3?
If the rate of change of volume of a sphere is equal to the rate of change of its radius then the surface area of a sphere is ____________.
What is the rate of change of the area of a circle with respect to its radius when, r = 3 cm
An edge of a variable cube is increasing at the rate of 10 cm/sec. How fast will the volume of the cube increase if the edge is 5 cm long?
