Advertisements
Advertisements
प्रश्न
A ladder, 5 meter long, standing on a horizontal floor, leans against a vertical wall. If the top of the ladder slides downwards at the rate of 10 cm/sec, then the rate at which the angle between the floor and the ladder is decreasing when lower end of ladder is 2 metres from the wall is ______.
विकल्प
1/10` radian/sec
1/20 radian/sec
20 radian/sec
10 radian/sec
उत्तर
A ladder, 5 meter long, standing on a horizontal floor, leans against a vertical wall. If the top of the ladder slides downwards at the rate of 10 cm/sec, then the rate at which the angle between the floor and the ladder is decreasing when lower end of ladder is 2 metres from the wall is 1/20 radian/sec.
Explanation: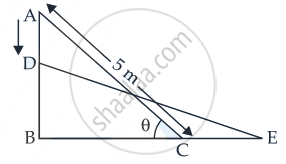
Length of ladder = 5 m
Let AB = y m and BC = x m
∴ In right ΔABC,
AB2 + BC2 = AC2
⇒ x2 + y2 = (5)2
⇒ x2 + y2 = 25
Differentiating both sides w.r.t x, we have
`2x * "dx"/"dt" + 2y * "dy"/"dt"` = 0
⇒ `x "dx"/"dt" + y * "dy"/"dt"` = 0
⇒ `2 * "dx"/"dt" + y xx (-0.1)` = 0 ....[∵ x = 2m]
⇒ `2 * "dx"/"dt" + sqrt(25 - x^2) xx (-0.1)` = 0
⇒ `2 * "dx"/"dt" + sqrt(25 - 4) xx (-0.1)` = 0
⇒ `2 * "dx"/"dt" - sqrt(21)/10` = 0
⇒ `"dx"/"dt" = sqrt(21)/20`
Now cos θ = `"BC"/"AC"` ....(θ is in radian)
⇒ cos θ = `x/5`
Differentiating both sides w.r.t. t, we get
`"d"/"dt" cos theta = 1/5 * "dx"/"dt"`
⇒ `- sin theta ("d"theta)/"dt" = 1/5 * sqrt(21)/20`
⇒ `("d"theta)/"dt" = sqrt(21)/100 xx (- 1/sin theta)`
= `sqrt(21)/100 xx -(1/("AB"/"AC"))`
= `- sqrt(21)/100 xx "AC"/"AB"`
= `- sqrt(21)/100 xx 5/sqrt(21)`
= `- 1/20` radian/sec
[(–) sign shows the decrease of change of angle]
Hence, the required rate = `1/20` radian/sec
APPEARS IN
संबंधित प्रश्न
The radius of a circle is increasing at the rate of 0.7 cm/s. What is the rate of increase of its circumference?
The length x of a rectangle is decreasing at the rate of 5 cm/minute and the width y is increasing at the rate of 4 cm/minute. When x = 8 cm and y = 6 cm, find the rates of change of (a) the perimeter, and (b) the area of the rectangle.
The total cost C(x) in rupees associated with the production of x units of an item is given by C(x) = 0.007x3 – 0.003x2 + 15x + 4000. Find the marginal cost when 17 units are produced
The rate of change of the area of a circle with respect to its radius r at r = 6 cm is ______.
The two equal sides of an isosceles triangle with fixed base b are decreasing at the rate of 3 cm per second. How fast is the area decreasing when the two equal sides are equal to the base?
The total cost C(x) associated with the production of x units of an item is given by C(x) = 0.005x3 – 0.02x2 + 30x + 5000. Find the marginal cost when 3 units are produced, whereby marginal cost we mean the instantaneous rate of change of total cost at any level of output.
Find the rate of change of the volume of a sphere with respect to its diameter ?
Find the rate of change of the area of a circle with respect to its radius r when r = 5 cm
The radius of a circle is increasing at the rate of 0.7 cm/sec. What is the rate of increase of its circumference?
The radius of an air bubble is increasing at the rate of 0.5 cm/sec. At what rate is the volume of the bubble increasing when the radius is 1 cm?
A stone is dropped into a quiet lake and waves move in circles at a speed of 4 cm/sec. At the instant when the radius of the circular wave is 10 cm, how fast is the enclosed area increasing?
A man 160 cm tall, walks away from a source of light situated at the top of a pole 6 m high, at the rate of 1.1 m/sec. How fast is the length of his shadow increasing when he is 1 m away from the pole?
A ladder 13 m long leans against a wall. The foot of the ladder is pulled along the ground away from the wall, at the rate of 1.5 m/sec. How fast is the angle θ between the ladder and the ground is changing when the foot of the ladder is 12 m away from the wall.
Water is running into an inverted cone at the rate of π cubic metres per minute. The height of the cone is 10 metres, and the radius of its base is 5 m. How fast the water level is rising when the water stands 7.5 m below the base.
Find the point on the curve y2 = 8x for which the abscissa and ordinate change at the same rate ?
The radius of a circle is increasing at the rate of 0.5 cm/sec. Find the rate of increase of its circumference ?
The radius of the base of a cone is increasing at the rate of 3 cm/minute and the altitude is decreasing at the rate of 4 cm/minute. The rate of change of lateral surface when the radius = 7 cm and altitude 24 cm is
The radius of a sphere is increasing at the rate of 0.2 cm/sec. The rate at which the volume of the sphere increase when radius is 15 cm, is
The volume of a sphere is increasing at 3 cm3/sec. The rate at which the radius increases when radius is 2 cm, is
The volume of a sphere is increasing at the rate of 4π cm3/sec. The rate of increase of the radius when the volume is 288 π cm3, is
If the rate of change of volume of a sphere is equal to the rate of change of its radius, then its radius is equal to
The diameter of a circle is increasing at the rate of 1 cm/sec. When its radius is π, the rate of increase of its area is
A man 2 metres tall walks away from a lamp post 5 metres height at the rate of 4.8 km/hr. The rate of increase of the length of his shadow is
In a sphere the rate of change of surface area is
If the area of a circle increases at a uniform rate, then prove that perimeter varies inversely as the radius
A particle is moving along the curve x = at2 + bt + c. If ac = b2, then particle would be moving with uniform ____________.
If the circumference of circle is increasing at the constant rate, prove that rate of change of area of circle is directly proportional to its radius.
If equal sides of an isosceles triangle with fixed base 10 cm are increasing at the rate of 4 cm/sec, how fast is the area of triangle increasing at an instant when all sides become equal?
An edge of a variable cube is increasing at the rate of 10 cm/sec. How fast will the volume of the cube increase if the edge is 5 cm long?
