Advertisements
Advertisements
प्रश्न
A man 2 metres tall walks away from a lamp post 5 metres height at the rate of 4.8 km/hr. The rate of increase of the length of his shadow is
विकल्प
1.6 km/hr
6.3 km/hr
5 km/hr
3.2 km/hr
उत्तर
Let AB be the lamp post. Suppose at any time t, the man CD be at a distance of x km from the lamp post and y m be the length of his shadow CE.
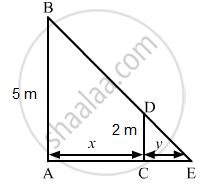
\[\text { Since triangles ABE and CDE are similar }, \]
\[\frac{AB}{CD} = \frac{AE}{CE}\]
\[\Rightarrow \frac{5}{2} = \frac{x + y}{y}\]
\[ \Rightarrow \frac{x}{y} = \frac{5}{2} - 1\]
\[ \Rightarrow \frac{x}{y} = \frac{3}{2}\]
\[ \Rightarrow y = \frac{2}{3}x\]
\[ \Rightarrow \frac{dy}{dt} = \frac{2}{3}\left( \frac{dx}{dt} \right)\]
\[ \Rightarrow \frac{dy}{dt} = \frac{2}{3} \times 4 . 8\]
\[ \Rightarrow \frac{dy}{dt} = 3 . 2 \ km/hr\]
APPEARS IN
संबंधित प्रश्न
A point source of light is hung 30 feet directly above a straight horizontal path on which a man of 6 feet in height is walking. How fast will the man’s shadow lengthen and how fast will the tip of shadow move when he is walking away from the light at the rate of 100 ft/min.
The rate of growth of bacteria is proportional to the number present. If, initially, there were
1000 bacteria and the number doubles in one hour, find the number of bacteria after 2½
hours.
[Take `sqrt2` = 1.414]
Find the rate of change of the area of a circle with respect to its radius r when r = 3 cm.
The radius of a circle is increasing at the rate of 0.7 cm/s. What is the rate of increase of its circumference?
The total cost C(x) in rupees associated with the production of x units of an item is given by C(x) = 0.007x3 – 0.003x2 + 15x + 4000. Find the marginal cost when 17 units are produced
The total revenue in rupees received from the sale of x units of a product is given by R(x) = 13x2 + 26x + 15. Find the marginal revenue when x = 7.
The total revenue in rupees received from the sale of x units of a product is given by R(x) = 3x2 + 36x + 5. The marginal revenue, when x = 15 is ______.
Find the rate of change of the volume of a sphere with respect to its surface area when the radius is 2 cm ?
Find the rate of change of the volume of a ball with respect to its radius r. How fast is the volume changing with respect to the radius when the radius is 2 cm?
An edge of a variable cube is increasing at the rate of 3 cm per second. How fast is the volume of the cube increasing when the edge is 10 cm long?
A balloon which always remains spherical, is being inflated by pumping in 900 cubic centimetres of gas per second. Find the rate at which the radius of the balloon is increasing when the radius is 15 cm.
A stone is dropped into a quiet lake and waves move in circles at a speed of 4 cm/sec. At the instant when the radius of the circular wave is 10 cm, how fast is the enclosed area increasing?
A particle moves along the curve y = x2 + 2x. At what point(s) on the curve are the x and y coordinates of the particle changing at the same rate?
The length x of a rectangle is decreasing at the rate of 5 cm/minute and the width y is increasing at the rate of 4 cm/minute. When x = 8 cm and y = 6 cm, find the rates of change of the perimeter.
If a particle moves in a straight line such that the distance travelled in time t is given by s = t3 − 6t2+ 9t + 8. Find the initial velocity of the particle ?
The sides of an equilateral triangle are increasing at the rate of 2 cm/sec. How far is the area increasing when the side is 10 cms?
The altitude of a cone is 20 cm and its semi-vertical angle is 30°. If the semi-vertical angle is increasing at the rate of 2° per second, then the radius of the base is increasing at the rate of
The radius of the base of a cone is increasing at the rate of 3 cm/minute and the altitude is decreasing at the rate of 4 cm/minute. The rate of change of lateral surface when the radius = 7 cm and altitude 24 cm is
If the rate of change of area of a circle is equal to the rate of change of its diameter, then its radius is equal to
Each side of an equilateral triangle is increasing at the rate of 8 cm/hr. The rate of increase of its area when side is 2 cm, is
If s = t3 − 4t2 + 5 describes the motion of a particle, then its velocity when the acceleration vanishes, is
Find the rate of change of the area of a circle with respect to its radius r when r = 4 cm.
A 13 m long ladder is leaning against a wall, touching the wall at a certain height from the ground level. The bottom of the ladder is pulled away from the wall, along the ground, at the rate of 2 m/s. How fast is the height on the wall decreasing when the foot of the ladder is 5 m away from the wall?
A ladder 13 m long is leaning against a vertical wall. The bottom of the ladder is dragged away from the wall along the ground at the rate of 2 cm/sec. How fast is the height on the wall decreasing when the foot of the ladder is 5 m away from the wall.
For the curve y = 5x – 2x3, if x increases at the rate of 2 units/sec, then how fast is the slope of curve changing when x = 3?
If the area of a circle increases at a uniform rate, then prove that perimeter varies inversely as the radius
Two men A and B start with velocities v at the same time from the junction of two roads inclined at 45° to each other. If they travel by different roads, find the rate at which they are being seperated.
A swimming pool is to be drained for cleaning. If L represents the number of litres of water in the pool t seconds after the pool has been plugged off to drain and L = 200 (10 – t)2. How fast is the water running out at the end of 5 seconds? What is the average rate at which the water flows out during the first 5 seconds?
The volume of a cube increases at a constant rate. Prove that the increase in its surface area varies inversely as the length of the side
A ladder, 5 meter long, standing on a horizontal floor, leans against a vertical wall. If the top of the ladder slides downwards at the rate of 10 cm/sec, then the rate at which the angle between the floor and the ladder is decreasing when lower end of ladder is 2 metres from the wall is ______.
If the rate of change of the area of the circle is equal to the rate of change of its diameter then its radius is equal to ____________.
The rate of change of volume of a sphere is equal to the rate of change of the radius than its radius equal to ____________.
The radius of a circle is increasing uniformly at the rate of 3 cm per second. Find the rate at which the area of the circle is increasing when the radius is 10 cm.
A spherical balloon is being inflated at the rate of 35 cc/min. The rate of increase in the surface area (in cm2/min.) of the balloon when its diameter is 14 cm, is ______.
Given that `1/y + 1/x = 1/12` and y decreases at a rate of 1 cms–1, find the rate of change of x when x = 5 cm and y = 1 cm.
