Advertisements
Advertisements
प्रश्न
A point source of light is hung 30 feet directly above a straight horizontal path on which a man of 6 feet in height is walking. How fast will the man’s shadow lengthen and how fast will the tip of shadow move when he is walking away from the light at the rate of 100 ft/min.
उत्तर
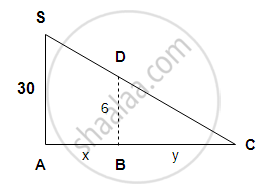
Let S be the position of source of light.
Let BD be the position of the man at a time t.
Let AB = x and BC = length of the shadow = y
Now
`dx/dt=100`
From the ∆ASC ~ ∆BDC
`:.(AS)/(BD)=(AC)/(BC)`
`30/6=(x+y)/y`
∴ 5y = x+ y
4y = x
`4 "dy"/"dt" = "dx"/"dt"`
`:.dy/dt =1/4(100)=25`
∴ The shadow of the man is lengthening at the rate 25 ft/min
The tip of shadow is at C. Let AC = z.
∴ AB = c
`(AS)/(BD)=(AC)/(BC)`
∴ BC = z – x
`:.30/6=z/(z-x)`
5z – 5x = z
4z = 5x
`4 "dz"/"dt" = 5 "dx"/"dt"`
`4 "dz"/"dt" = 5 xx 100 `
`"dz"/"dt" = 5 xx 25 = 125`
The tip of the shadow is moving at the rate 125 ft/min.
APPEARS IN
संबंधित प्रश्न
If y = f (u) is a differential function of u and u = g(x) is a differential function of x, then prove that y = f [g(x)] is a differential function of x and `dy/dx=dy/(du) xx (du)/dx`
A balloon, which always remains spherical on inflation, is being inflated by pumping in 900 cubic centimetres of gas per second. Find the rate at which the radius of the balloon increases when the radius is 15 cm.
A balloon, which always remains spherical has a variable radius. Find the rate at which its volume is increasing with the radius when the later is 10 cm.
A ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2 cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall?
A particle moves along the curve 6y = x3 +2. Find the points on the curve at which the y-coordinate is changing 8 times as fast as the x-coordinate.
The total cost C(x) in rupees associated with the production of x units of an item is given by C(x) = 0.007x3 – 0.003x2 + 15x + 4000. Find the marginal cost when 17 units are produced
The rate of change of the area of a circle with respect to its radius r at r = 6 cm is ______.
The total revenue in rupees received from the sale of x units of a product is given by R(x) = 3x2 + 36x + 5. The marginal revenue, when x = 15 is ______.
The volume of a sphere is increasing at the rate of 8 cm3/s. Find the rate at which its surface area is increasing when the radius of the sphere is 12 cm.
The total cost C(x) associated with the production of x units of an item is given by C(x) = 0.005x3 – 0.02x2 + 30x + 5000. Find the marginal cost when 3 units are produced, whereby marginal cost we mean the instantaneous rate of change of total cost at any level of output.
Find the rate of change of the volume of a sphere with respect to its diameter ?
Find the rate of change of the volume of a ball with respect to its radius r. How fast is the volume changing with respect to the radius when the radius is 2 cm?
The side of a square is increasing at the rate of 0.2 cm/sec. Find the rate of increase of the perimeter of the square.
The volume of a cube is increasing at the rate of 9 cm3/sec. How fast is the surface area increasing when the length of an edge is 10 cm?
A circular disc of radius 3 cm is being heated. Due to expansion, its radius increases at the rate of 0.05 cm/sec. Find the rate at which its area is increasing when radius is 3.2 cm.
Find the surface area of a sphere when its volume is changing at the same rate as its radius ?
The amount of pollution content added in air in a city due to x diesel vehicles is given by P(x) = 0.005x3 + 0.02x2 + 30x. Find the marginal increase in pollution content when 3 diesel vehicles are added and write which value is indicated in the above questions ?
A ladder, 5 metre long, standing on a horizontal floor, leans against a vertical wall. If the top of the ladder slides down wards at the rate of 10 cm/sec, then find the rate at which the angle between the floor and ladder is decreasing when lower end of ladder is 2 metres from the wall ?
Side of an equilateral triangle expands at the rate of 2 cm/sec. The rate of increase of its area when each side is 10 cm is
A cylindrical vessel of radius 0.5 m is filled with oil at the rate of 0.25 π m3/minute. The rate at which the surface of the oil is rising, is
The coordinates of the point on the ellipse 16x2 + 9y2 = 400 where the ordinate decreases at the same rate at which the abscissa increases, are
If the rate of change of volume of a sphere is equal to the rate of change of its radius, then its radius is equal to
If s = t3 − 4t2 + 5 describes the motion of a particle, then its velocity when the acceleration vanishes, is
A man 2 metres tall walks away from a lamp post 5 metres height at the rate of 4.8 km/hr. The rate of increase of the length of his shadow is
In a sphere the rate of change of volume is
A cylindrical tank of radius 10 m is being filled with wheat at the rate of 314 cubic metre per hour. Then the depth of the wheat is increasing at the rate of
Evaluate: `int (x(1+x^2))/(1+x^4)dx`
A ladder 13 m long is leaning against a vertical wall. The bottom of the ladder is dragged away from the wall along the ground at the rate of 2 cm/sec. How fast is the height on the wall decreasing when the foot of the ladder is 5 m away from the wall.
Water is dripping out from a conical funnel of semi-vertical angle `pi/4` at the uniform rate of 2cm2/sec in the surface area, through a tiny hole at the vertex of the bottom. When the slant height of cone is 4 cm, find the rate of decrease of the slant height of water.
A ladder, 5 meter long, standing on a horizontal floor, leans against a vertical wall. If the top of the ladder slides downwards at the rate of 10 cm/sec, then the rate at which the angle between the floor and the ladder is decreasing when lower end of ladder is 2 metres from the wall is ______.
If the rate of change of the area of the circle is equal to the rate of change of its diameter then its radius is equal to ____________.
Let y = f(x) be a function. If the change in one quantity 'y’ varies with another quantity x, then which of the following denote the rate of change of y with respect to x.
A ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2 cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall?
The median of an equilateral triangle is increasing at the ratio of `2sqrt(3)` cm/s. Find the rate at which its side is increasing.
A kite is being pulled down by a string that goes through a ring on the ground 8 meters away from the person pulling it. If the string is pulled in at 1 meter per second, how fast is the kite coming down when it is 15 meters high?
