Advertisements
Advertisements
प्रश्न
A ball falls on the ground from a height of 2.0 m and rebounds up to a height of 1.5 m. Find the coefficient of restitution.
उत्तर
Let the velocity of the ball falling from height h1 be u (when it approaches the ground).
Velocity on the ground, \[u = \sqrt{2g h_1}\]
\[\Rightarrow v = \sqrt{2g h_2}\]
\[ = \sqrt{2 \times 9 . 8 \times 1 . 5}\]
Let the coefficient of restitution be e.
We know, v = eu
Hence, the coefficient of restitution is \[\frac{\sqrt{3}}{2}\] .
APPEARS IN
संबंधित प्रश्न
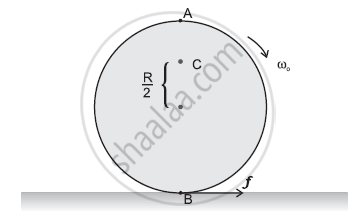
A disc rotating about its axis with angular speed ωois placed lightly (without any translational push) on a perfectly frictionless table. The radius of the disc is R. What are the linear velocities of the points A, B and C on the disc shown in Figure? Will the disc roll in the direction indicated?
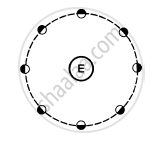
The moon rotates about the earth in such a way that only one hemisphere of the moon faces the earth (see the following figure). Can we ever see the "other face" of the moon from the earth? Can a person on the moon ever see all the faces of the earth?
A sphere rolls on a horizontal surface. If there any point of the sphere which has a vertical velocity?
A body is in pure rotation. The linear speed \[\nu\] of a particle, the distance r of the particle from the axis and the angular velocity \[\omega\] of the body are related as \[\omega = \frac{\nu}{r}.\] Thus
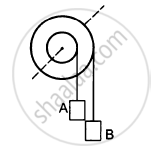
The following figure shows a small wheel fixed coaxially on a bigger one of double the radius. The system rotates about the common axis. The strings supporting A and B do not slip on the wheels. If x and y be the distance travelled by A and B in the same time interval, then _________ .
The angular velocity of the engine (and hence of the wheel) of a scooter is proportional to the petrol input per second. The scooter is moving on a frictionless road with uniform velocity. If the petrol input is increased by 10%, the linear velocity of the scooter is increased by ___________ .
A sphere is rolled on a rough horizontal surface. If gradually slows down and stops. The force of friction tries to
(a) decrease the linear velocity
(b) increase the angular velocity
(c) increase the linear momentum
(d) decrease the angular velocity.
Find the angular velocity of a body rotating with an acceleration of 2 rev/s2 as it completes the 5th revolution after the start.
A disc of radius 10 cm is rotating about its axis at an angular speed of 20 rad/s. Find the linear speed of a point on the rim.
A disc of radius 10 cm is rotating about its axis at an angular speed of 20 rad/s. Find the linear speed of the middle point of a radius.
A wheel rotating at a speed of 600 rpm (revolutions per minute) about its axis is brought to rest by applying a constant torque for 10 seconds. Find the angular deceleration and the angular velocity 5 seconds after the application of the torque.
Suppose the platform of the previous problem is brought to rest with the ball in the hand of the kid standing on the rim. The kid throws the ball horizontally to his friend in a direction tangential to the rim with a speed \[\nu\] as seen by his friend. Find the angular velocity with which the platform will start rotating.
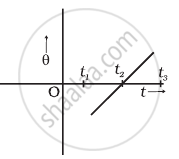
The variation of angular position θ, of a point on a rotating rigid body, with time t is shown in figure. Is the body rotating clock-wise or anti-clockwise?
Two cylindrical hollow drums of radii R and 2R, and of a common height h, are rotating with angular velocities ω(anti-clockwise) and ω(clockwise), respectively. Their axes, fixed are parallel and in a horizontal plane separated by (3R + δ). They are now brought in contact (δ → 0).
- Show the frictional forces just after contact.
- Identify forces and torques external to the system just after contact.
- What would be the ratio of final angular velocities when friction ceases?
