Advertisements
Advertisements
प्रश्न
A ball is thrown vertically upwards. It goes to a height 20 m and then returns to the ground. Taking acceleration due to gravity g to be 10 ms-2 , find :
the final velocity of the ball on reaching the ground .
उत्तर
Given, maximum height reached, s = 20 m
Acceleration due to gravity, g = 10 m/s2
Let v' be the final velocity of the ball on reaching the ground.
Considering the motion from the highest point to ground,
Velocity at highest point = 0 = Initial velocity for downward journey of the ball.
Distance travelled, s = 20m
Using the third equation of motion,
v2 - u2 = 2gs
or, v2 - 0 = 2 (10) (20) m/s
or, v2 = 400 m/s
or, v = 20 m/s
APPEARS IN
संबंधित प्रश्न
Write the formula to find the magnitude of the gravitational force between the earth and an object on the surface of the earth.
Choose the correct alternative:
Acceleration due to gravity is independent of mass of the earth/mass of the body.
Choose the correct answer from among the given ones:
For the problem 8.10, the direction of the gravitational intensity at an arbitrary point P is indicated by the arrow (i) d, (ii) e, (iii) f, (iv) g.
State two applications of universal law of gravitation.
Can you think of two particles which do not exert gravitational force on each other?
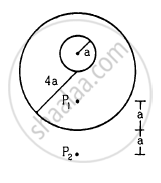
A uniform metal sphere of radius a and mass M is surrounded by a thin uniform spherical shell of equal mass and radius 4a (In the following figure). The centre of the shell falls on the surface of the inner sphere. Find the gravitational field at the points P1 and P2 shown in the figure.
Why don't you feel the force of attraction between your friend sitting close to you and yourself?
Name and state the action and reaction in the following case:
Hammering a nail.
State Newton's law of gravitation. What is the difference between:
g and G?
The gravitational force between a hollow spherical shell (of radius R and uniform density) and a point mass is F. Show the nature of F vs r graph where r is the distance of the point from the centre of the hollow spherical shell of uniform density.
