Advertisements
Advertisements
प्रश्न
A bat is flitting about in a cave, navigating via ultrasonic beeps. Assume that the sound emission frequency of the bat is 40 kHz. During one fast swoop directly toward a flat wall surface, the bat is moving at 0.03 times the speed of sound in air. What frequency does the bat hear reflected off the wall?
उत्तर १
Ultrasonic beep frequency emitted by the bat, ν = 40 kHz
Velocity of the bat, vb = 0.03 v
Where, v = velocity of sound in air
The apparent frequency of the sound striking the wall is given as:
`v' = (v/(v - v_b))v`
`= (v/(v - 0.03v)) xx 40`
`= 40/0.97` kHz`
This frequency is reflected by the stationary wall (`v_s = 0`) toward the bat.
The frequency (v") of the received sound is given by the relation:
`v" = ((v + v_b)/v) v'`
`= ((v+0.03v)/v) xx 40/0.97`
`= (1.03 xx 40)/ 0.97 = 42.47 kHz`
उत्तर २
Here, the frequency of sound emitted by the bat, υ = 40 kHz. Velocity of bat, υs = 0.03 υ, where υ is velocity of sound. Apparent frequency of sound striking the wall
v' = v/(v - v_s) xx v = v/(v - 0.03v) xx 40 kHz
= `40/0.97 kHz`
This frequency is reflected by the wall and is received by the bat moving towards the wall
So `v_s = 0`
`v_L = 0.03 v`
`v" = (v+v_L)/v xx v'= (v + 0.03v)/v (40/0.97)`
`= 1.03/0.97 xx 40 kHz = 42.47 kHz`
`:. y = (1,1) = 7.5 sin (732.81^@)`
`= 7.5 sin (90 xx 8 + 12.81^@) = 7.5 sin 12.81^@`
= 7.5 xx 0.2217
`= 1.6629 ~~ 1.663 cm`
The velocity of the oscillation at a given point and time is given as:
`v =d/(dt) y (x,t) = d/dt [7.5 sin(0.0050x + 12t + pi/4)]`
`= 7.5 xx 12 cos (0.0050x + 12t + pi/4)`
At x = 1 cm and t = 1 s.
`v = y(1,1)= 90 cos(0.0050x + 12t + pi/4)`
At x = 1 cm and t = 1 s
`v = y(1,1) = 90 cos (12.005 + pi/4)`
= 90 cos(732.81^@) = 90 cos(90xx8+ 12.81)
`= 90 cos(12.81^@)`
`= 90 xx 0.975 = 87.75 "cm/s"`
Now the equation of a propagating wave is given by
`y(x,t) = a sin(kx + wt + phi)`
Where
k = (2pi)/lambda
`:. lambda = (2pi)/k`
And `omega = 2piv`
`:. v = omega/(2pi)`
`Speed, v = vlambda = omega/k`
APPEARS IN
संबंधित प्रश्न
A pipe 20 cm long is closed at one end. Which harmonic mode of the pipe is resonantly excited by a 430 Hz source? Will the same source be in resonance with the pipe if both ends are open? (Speed of sound in air is 340 m s–1).
A 2 m long string fixed at both ends is set into vibrations in its first overtone. The wave speed on the string is 200 m s−1 and the amplitude is 0⋅5 cm. (a) Find the wavelength and the frequency. (b) Write the equation giving the displacement of different points as a function of time. Choose the X-axis along the string with the origin at one end and t = 0 at the instant when the point x = 50 cm has reached its maximum displacement.
The displacement of a string is given by y (x, t) = 0.06 sin (2πx/3) cos (120 πt) where x and y are in m and t in s. The length of the string is 1.5 m and its mass is 3.0 × 10−2 kg.
- It represents a progressive wave of frequency 60 Hz.
- It represents a stationary wave of frequency 60 Hz.
- It is the result of superposition of two waves of wavelength 3 m, frequency 60 Hz each travelling with a speed of 180 m/s in opposite direction.
- Amplitude of this wave is constant.
The wave pattern on a stretched string is shown in figure. Interpret what kind of wave this is and find its wavelength.

A tuning fork vibrating with a frequency of 512 Hz is kept close to the open end of a tube filled with water (Figure). The water level in the tube is gradually lowered. When the water level is 17 cm below the open end, maximum intensity of sound is heard. If the room temperature is 20°C, calculate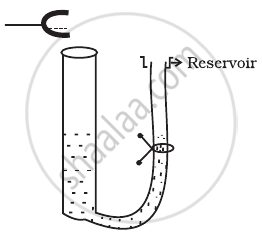
- speed of sound in air at room temperature
- speed of sound in air at 0°C
- if the water in the tube is replaced with mercury, will there be any difference in your observations?
Show that when a string fixed at its two ends vibrates in 1 loop, 2 loops, 3 loops and 4 loops, the frequencies are in the ratio 1:2:3:4.
Two identical strings X and Z made of same material have tension Tx and Tz in them If their fundamental frequencies are 450 Hz and 300 Hz, respectively, then the ratio `"T"_x/"T"_"z"` is ______.
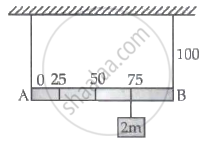
Shown in the figure is rigid and uniform one meter long rod AB held in horizontal position by two strings tied to its ends and attached to the ceiling. The rod is of mass 'm' and has another weight of mass 2m hung at a distance of 75 cm from A. The tension in the string at A is :
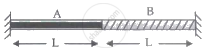
A wire of length 2L is made by joining two wires A and B of the same length but different radii r and 2r, and made of the same material. It is vibrating at a frequency such that the joint of the two wires forms a node. If the number of antinodes in wire A is p and that in B is q then the ratio p : q is ______.
A tuning fork is vibrating at 250 Hz. The length of the shortest closed organ pipe that will resonate with the tuning fork will be ______ cm.
(Take the speed of sound in air as 340 ms-1.)
