Advertisements
Advertisements
प्रश्न
A pipe 20 cm long is closed at one end. Which harmonic mode of the pipe is resonantly excited by a 430 Hz source? Will the same source be in resonance with the pipe if both ends are open? (Speed of sound in air is 340 m s–1).
उत्तर १
First (Fundamental); No
Length of the pipe, l = 20 cm = 0.2 m
Source frequency = nth normal mode of frequency, νn = 430 Hz
Speed of sound, v = 340 m/s
In a closed pipe, the nth normal mode of frequency is given by the relation:
`v_n = (2n - 1) v/(4l)` n is an interger = 0,1.2.3
`430 =(2n - 1) 340/(4xx0.2)`
`2n -1 = (430xx4xx0.2)/340 = 1.01`
2n = 2.01
n ~ 1
Hence, the first mode of vibration frequency is resonantly excited by the given source. In a pipe open at both ends, the nth mode of vibration frequency is given by the relation:
`v_n = "nv"/(2l)`
`n = (2lv_n)/v`
`= (2xx0.2xx430)/340 = 0.5`
Since the number of the mode of vibration (n) has to be an integer, the given source does not produce a resonant vibration in an open pipe.
उत्तर २
Here length of pipe, 1 = 20 cm = 0.20 m, frequency v = 430 Hz and speed of sound in air υ = 340 ms-1
For closed end pipe, `v = ((2n - 1)v)/(4l)` where n = 1, 2, 3.....
`:. (2n -1) = (4vl)/v = (4xx430xx0.20)/340 = 1.02`
`=> 2n = 1.02 + 1= 2.02 => n = 0.20/2 = 1.01`
Hence, resonance can occur only for first (or fundamental) mode of vibration.
As for an open pipe ` v = (nv)/(2l)` where n = 1, 2,3 ....
`:. n = (2lv)/v = (2xx430xx0.20)/(340) = 0.51`
As n < 1, hence in this case resonance position cannot be obtained
APPEARS IN
संबंधित प्रश्न
The number of possible natural oscillations of the air column in a pipe closed at one end of length 85 cm whose frequencies lie below 1250 Hz? (v = 340 m/s)
The displacement of a string is given by y (x, t) = 0.06 sin (2πx/3) cos (120 πt) where x and y are in m and t in s. The length of the string is 1.5 m and its mass is 3.0 × 10−2 kg.
- It represents a progressive wave of frequency 60 Hz.
- It represents a stationary wave of frequency 60 Hz.
- It is the result of superposition of two waves of wavelength 3 m, frequency 60 Hz each travelling with a speed of 180 m/s in opposite direction.
- Amplitude of this wave is constant.
The transverse displacement of a string (clamped at its both ends) is given by y(x, t) = 0.06 sin (2πx/3) cos (120 πt). All the points on the string between two consecutive nodes vibrate with ______.
- same frequency
- same phase
- same energy
- different amplitude.
An organ pipe of length L open at both ends is found to vibrate in its first harmonic when sounded with a tuning fork of 480 Hz. What should be the length of a pipe closed at one end, so that it also vibrates in its first harmonic with the same tuning fork?
A pipe 20 cm long is closed at one end. Which harmonic mode of the pipe is resonantly excited by a source of 1237.5 Hz? (sound velocity in air = 330 ms–1)
The wave pattern on a stretched string is shown in figure. Interpret what kind of wave this is and find its wavelength.

A tuning fork vibrating with a frequency of 512 Hz is kept close to the open end of a tube filled with water (Figure). The water level in the tube is gradually lowered. When the water level is 17 cm below the open end, maximum intensity of sound is heard. If the room temperature is 20°C, calculate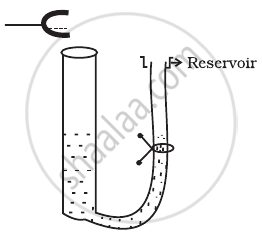
- speed of sound in air at room temperature
- speed of sound in air at 0°C
- if the water in the tube is replaced with mercury, will there be any difference in your observations?
Show that when a string fixed at its two ends vibrates in 1 loop, 2 loops, 3 loops and 4 loops, the frequencies are in the ratio 1:2:3:4.
Two travelling waves produce a standing wave represented by the equation. y = 1.0 mm cos (1.57 cm-1) x sin (78.5 s-1)t. The node closest to the origin in the region x > 0 will be at x = ______ cm.
A tuning fork is vibrating at 250 Hz. The length of the shortest closed organ pipe that will resonate with the tuning fork will be ______ cm.
(Take the speed of sound in air as 340 ms-1.)
