Advertisements
Advertisements
Question
A pipe 20 cm long is closed at one end. Which harmonic mode of the pipe is resonantly excited by a 430 Hz source? Will the same source be in resonance with the pipe if both ends are open? (Speed of sound in air is 340 m s–1).
Solution 1
First (Fundamental); No
Length of the pipe, l = 20 cm = 0.2 m
Source frequency = nth normal mode of frequency, νn = 430 Hz
Speed of sound, v = 340 m/s
In a closed pipe, the nth normal mode of frequency is given by the relation:
`v_n = (2n - 1) v/(4l)` n is an interger = 0,1.2.3
`430 =(2n - 1) 340/(4xx0.2)`
`2n -1 = (430xx4xx0.2)/340 = 1.01`
2n = 2.01
n ~ 1
Hence, the first mode of vibration frequency is resonantly excited by the given source. In a pipe open at both ends, the nth mode of vibration frequency is given by the relation:
`v_n = "nv"/(2l)`
`n = (2lv_n)/v`
`= (2xx0.2xx430)/340 = 0.5`
Since the number of the mode of vibration (n) has to be an integer, the given source does not produce a resonant vibration in an open pipe.
Solution 2
Here length of pipe, 1 = 20 cm = 0.20 m, frequency v = 430 Hz and speed of sound in air υ = 340 ms-1
For closed end pipe, `v = ((2n - 1)v)/(4l)` where n = 1, 2, 3.....
`:. (2n -1) = (4vl)/v = (4xx430xx0.20)/340 = 1.02`
`=> 2n = 1.02 + 1= 2.02 => n = 0.20/2 = 1.01`
Hence, resonance can occur only for first (or fundamental) mode of vibration.
As for an open pipe ` v = (nv)/(2l)` where n = 1, 2,3 ....
`:. n = (2lv)/v = (2xx430xx0.20)/(340) = 0.51`
As n < 1, hence in this case resonance position cannot be obtained
APPEARS IN
RELATED QUESTIONS
A 2 m long string fixed at both ends is set into vibrations in its first overtone. The wave speed on the string is 200 m s−1 and the amplitude is 0⋅5 cm. (a) Find the wavelength and the frequency. (b) Write the equation giving the displacement of different points as a function of time. Choose the X-axis along the string with the origin at one end and t = 0 at the instant when the point x = 50 cm has reached its maximum displacement.
Two wires of same material are vibrating under the same tension. If the first overtone of first wire is equal to the second overtone of second wire and radius of first wire is twice the radius of the second then the ratio of length of first wire to second wire is
The number of possible natural oscillations of the air column in a pipe closed at one end of length 85 cm whose frequencies lie below 1250 Hz? (v = 340 m/s)
The displacement of a string is given by y (x, t) = 0.06 sin (2πx/3) cos (120 πt) where x and y are in m and t in s. The length of the string is 1.5 m and its mass is 3.0 × 10−2 kg.
- It represents a progressive wave of frequency 60 Hz.
- It represents a stationary wave of frequency 60 Hz.
- It is the result of superposition of two waves of wavelength 3 m, frequency 60 Hz each travelling with a speed of 180 m/s in opposite direction.
- Amplitude of this wave is constant.
Which of the following statements are true for a stationary wave?
- Every particle has a fixed amplitude which is different from the amplitude of its nearest particle.
- All the particles cross their mean position at the same time.
- All the particles are oscillating with same amplitude.
- There is no net transfer of energy across any plane.
- There are some particles which are always at rest.
A tuning fork vibrating with a frequency of 512 Hz is kept close to the open end of a tube filled with water (Figure). The water level in the tube is gradually lowered. When the water level is 17 cm below the open end, maximum intensity of sound is heard. If the room temperature is 20°C, calculate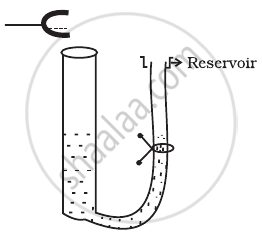
- speed of sound in air at room temperature
- speed of sound in air at 0°C
- if the water in the tube is replaced with mercury, will there be any difference in your observations?
Show that when a string fixed at its two ends vibrates in 1 loop, 2 loops, 3 loops and 4 loops, the frequencies are in the ratio 1:2:3:4.
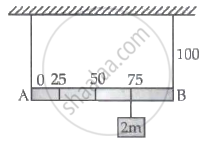
Shown in the figure is rigid and uniform one meter long rod AB held in horizontal position by two strings tied to its ends and attached to the ceiling. The rod is of mass 'm' and has another weight of mass 2m hung at a distance of 75 cm from A. The tension in the string at A is :
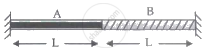
A wire of length 2L is made by joining two wires A and B of the same length but different radii r and 2r, and made of the same material. It is vibrating at a frequency such that the joint of the two wires forms a node. If the number of antinodes in wire A is p and that in B is q then the ratio p : q is ______.
A string 2.0 m long and fixed at its ends is driven by a 240 Hz vibrator. The string vibrates in its third harmonic mode. The speed of the wave and its fundamental frequency is ______.
