Advertisements
Advertisements
प्रश्न
A block is projected along a rough horizontal road with a speed of 10 m/s. If the coefficient of kinetic friction is 0.10, how far will it travel before coming to rest?
उत्तर
Friction force acting on the block will decelerate it.
Let the deceleration be 'a'.
Using free body diagram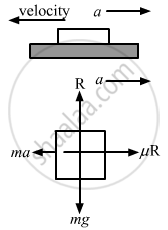
R − mg = 0
(where R is the normal reaction force)
⇒ R = mg (1)
Again, ma − μkR = 0
(where μk is the coefficient of kinetic friction)
From Equation (1),
⇒ ma = μkmg
⇒ a = μkg = 0.1 × 10
= 1 m/s2
Given:
initial velocity, u = 10 m/s
final velocity, v = 0 m/s (block comes to rest)
a = −1 m/s2 (deceleration)
Using equation of motion v2 - u2 = 2as
(where s is the distance travelled before coming to rest)
`s=(v^2-u^2)/(2a)`
On substituting the respective values, we get
`=0-10^2/2(-1)`
`=100/2=50"m"`
Therefore, the block will travel 50 m before coming to rest.
APPEARS IN
संबंधित प्रश्न
In a situation the contact force by a rough horizontal surface on a body placed on it has constant magnitude. If the angle between this force and the vertical is decreased, the frictional force between the surface and the body will
A block A kept on an inclined surface just begins to slide if the inclination is 30°. The block is replaced by another block B and it is found that it just begins to slide if the inclination is 40°.
Let F, FN and f denote the magnitudes of the contact force, normal force and the friction exerted by one surface on the other kept in contact. If none of these is zero.
(a) F > FN
(b) F > f
(c) FN > f
(d) FN − f < F < FN + f.
The contact force exerted by a body A on another body B is equal to the normal force between the bodies We conclude that
(a) the surface must be frictionless
(b) the force of friction between the bodies is zero
(c) the magnitude of normal force equal that of friction
(d) the bodies may be rough but they don't slip on each other.
A block of mass m is kept on a horizontal table. If the static friction coefficient is μ, find the frictional force acting on the block.
Suppose the block of the previous problem is pushed down the incline with a force of 4 N. How far will the block move in the first two seconds after starting from rest? The mass of the block is 4 kg.
In a children-park an inclined plane is constructed with an angle of incline 45° in the middle part (in the following figure). Find the acceleration of boy sliding on it if the friction coefficient between the cloth of the boy and the incline is 0.6 and g = 19 m/s2.

The angle between the resultant contact force and the normal force exerted by a body on the other is called the angle of friction. Show that, if λ be the angle of friction and μ the coefficient of static friction λ ≤ tan−1 μ.
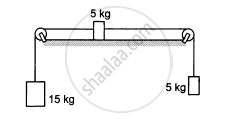
The friction co-efficient between the table and the block shown in the following figure is 0.2. Find the tensions in the two strings.
Two masses M1 and M2 are connected by a light rod and the system is slipping down a rough incline of angle θ with the horizontal. The friction coefficient at both the contacts is μ. Find the acceleration of the system and the force by the rod on one of the blocks.
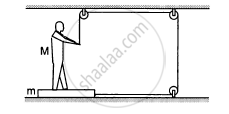
The friction coefficient between the board and the floor shown in the following figure is μ. Find the maximum force that the man can exert on the rope so that the board does not slip on the floor.
The friction coefficient between the two blocks shown in the following figure is μ but the floor is smooth. (a) What maximum horizontal force F can be applied without disturbing the equilibrium of the system? (b) Suppose the horizontal force applied is double of that found in part (a). Find the accelerations of the two masses.
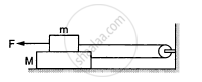
Suppose the entire system of the previous questions is kept inside an elevator which is coming down with an acceleration a < g. Repeat parts (a) and (b).
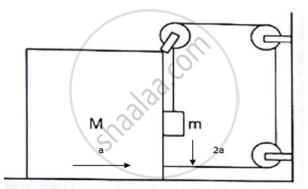
Find the acceleration of the block of mass M in the situation of figure in the following. The coefficient of friction between the two blocks is μ1 and that between the bigger block and the ground is μ2.
A block placed on a rough horizontal surface is pulled by a horizontal force F. Let f be the force applied by the rough surface on the block. Plot a graph of f versus F.
The coefficient of static friction between a wooden block of mass 0.5 kg and a vertical rough wall is 0.2. The magnitude of horizontal force that should be applied on the block to keep it adhered to the wall will be ______ N. [g = 10 ms-2]
An inclined plane is bent in such a way that the vertical cross-section is given by Y = `x^2/4` where y is in vertical and x in horizontal direction. If the upper surface of this curved plane is rough with coefficient of friction µ = 0.5, the maximum height in cm at which a stationary block will not slip downward is ______ cm.
