Advertisements
Advertisements
प्रश्न
A block is projected along a rough horizontal road with a speed of 10 m/s. If the coefficient of kinetic friction is 0.10, how far will it travel before coming to rest?
उत्तर
Friction force acting on the block will decelerate it.
Let the deceleration be 'a'.
Using free body diagram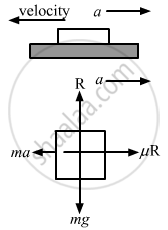
R − mg = 0
(where R is the normal reaction force)
⇒ R = mg (1)
Again, ma − μkR = 0
(where μk is the coefficient of kinetic friction)
From Equation (1),
⇒ ma = μkmg
⇒ a = μkg = 0.1 × 10
= 1 m/s2
Given:
initial velocity, u = 10 m/s
final velocity, v = 0 m/s (block comes to rest)
a = −1 m/s2 (deceleration)
Using equation of motion v2 - u2 = 2as
(where s is the distance travelled before coming to rest)
`s=(v^2-u^2)/(2a)`
On substituting the respective values, we get
`=0-10^2/2(-1)`
`=100/2=50"m"`
Therefore, the block will travel 50 m before coming to rest.
APPEARS IN
संबंधित प्रश्न
In a situation the contact force by a rough horizontal surface on a body placed on it has constant magnitude. If the angle between this force and the vertical is decreased, the frictional force between the surface and the body will
A boy of mass M is applying a horizontal force to slide a box of mass M' on a rough horizontal surface. The coefficient of friction between the shoes of the boy and the floor is μ and that between the box and the floor is μ'. In which of the following cases it is certainly not possible to slide the box?
Let F, FN and f denote the magnitudes of the contact force, normal force and the friction exerted by one surface on the other kept in contact. If none of these is zero.
(a) F > FN
(b) F > f
(c) FN > f
(d) FN − f < F < FN + f.
A body starts slipping down an incline and moves half metre in half second. How long will it take to move the next half metre?
The angle between the resultant contact force and the normal force exerted by a body on the other is called the angle of friction. Show that, if λ be the angle of friction and μ the coefficient of static friction λ ≤ tan−1 μ.
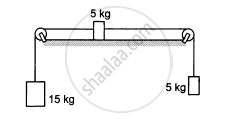
The friction co-efficient between the table and the block shown in the following figure is 0.2. Find the tensions in the two strings.
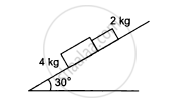
In the following figure shows two blocks in contact sliding down an inclined surface of inclination 30°. The friction coefficient between the block of mass 2.0 kg and the incline is μ1, and that between the block of mass 4.0 kg and incline is μ2. Calculate the acceleration of the 2.0 kg block if (a) μ1 = 0.20 and μ2 = 0.30, (b) μ1 = 0.30 and μ2 = 0.20. Take g = 10 m/s2.
Two masses M1 and M2 are connected by a light rod and the system is slipping down a rough incline of angle θ with the horizontal. The friction coefficient at both the contacts is μ. Find the acceleration of the system and the force by the rod on one of the blocks.
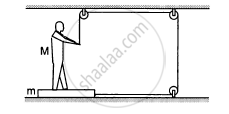
The friction coefficient between the board and the floor shown in the following figure is μ. Find the maximum force that the man can exert on the rope so that the board does not slip on the floor.
Find the accelerations a1, a2, a3 of the three blocks shown in the following figure if a horizontal force of 10 N is applied on (a) 2 kg block, (b) 3 kg block, (c) 7 kg block. Take g = 10 m/s2.
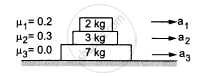
Suppose the entire system of the previous questions is kept inside an elevator which is coming down with an acceleration a < g. Repeat parts (a) and (b).
A block of mass m slips on a rough horizontal table under the action of a horizontal force applied to it. The coefficient of friction between the block and the table is μ. The table does not move on the floor. Find the total frictional force applied by the floor on the legs of the table. Do you need the friction coefficient between the table and the floor or the mass of the table?
A block of mass 2 kg is pushed against a rough vertical wall with a force of 40 N, coefficient of static friction being 0.5. Another horizontal force of 15 N, is applied on the block in a direction parallel to the wall. Will the block move? If yes, in which direction? If no, find the frictional force exerted by the wall on the block.
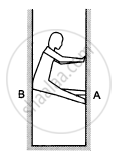
A person (40 kg) is managing to be at rest between two vertical walls by pressing one wall A by his hands and feet and the other wall B by his back (in the following figure). Assume that the friction coefficient between his body and the walls is 0.8 and that limiting friction acts at all the contacts. (a) Show that the person pushes the two wall with equal force. (b) Find the normal force exerted by either wall on the person. Take g = 10 m/s2.
A block placed on a rough horizontal surface is pulled by a horizontal force F. Let f be the force applied by the rough surface on the block. Plot a graph of f versus F.
The coefficient of static friction between a wooden block of mass 0.5 kg and a vertical rough wall is 0.2. The magnitude of horizontal force that should be applied on the block to keep it adhered to the wall will be ______ N. [g = 10 ms-2]
An inclined plane is bent in such a way that the vertical cross-section is given by Y = `x^2/4` where y is in vertical and x in horizontal direction. If the upper surface of this curved plane is rough with coefficient of friction µ = 0.5, the maximum height in cm at which a stationary block will not slip downward is ______ cm.
