Advertisements
Advertisements
प्रश्न
A box of 1.00 m3 is filled with nitrogen at 1.50 atm at 300K. The box has a hole of an area 0.010 mm2. How much time is required for the pressure to reduce by 0.10 atm, if the pressure outside is 1 atm.
उत्तर
The volume of the box `V_1 = 1 m^3`
Initial pressure `P_1 = 1.5 atm`
Final pressure `P_2^' = 1.5 - 0.1 = 1.4 atm`
Air pressure outside box `P_2 = 1 atm`
Initial temperature `T_1 = 300 K`
Final temperature `T_2 = 300 K`
a = area of hole = 0.01 mm2
= `0.01 xx 10^-6m^2`
= `10^-8m^2`
The initial pressure difference between atmosphere and tyre
`ΔP = (1.5 - 1) atm`
Mass of N2 gas molecule = `(0.028 Kg)/(6.023 xx 10^23)`
= `46.5 xx 10^-27 Kg`
`K_B = 1.38 xx 10^-23`
Assuming `ρ_(i n)` be the initial number of N2 gas molecules per unit volume at time Δt and also `v_(ix)` be the speed of molecules along the x-axis
At time Δt, the number of molecules colliding to the opposite wall
`1/2 ρ_(i n) [(v_(ix)) Δt]A`
Half is multiple as half molecule will strike the opposite wall
`v_(rms)^2 (N_2 "molecules") = v_(ix)^2 + v_(iy)^2 + v_(iz)^2`
∴ `|v_(ix)| = |v_(iy)| = |v_(iz)|`
Thus, `v_(rms)^2 = 3v_(ix)^2`
K.E. of gas molecule = `3/2 K_BT`
`1/2 mv_(rms)^2 = 3/2 K_BT`
`m3v_(ix)^2 = 3K_BT`
`v_(ix) = sqrt((K_BT)/m` .....(A)
At time Δt, the number of N2 gas molecule striking to a wall outward = `1/2 ρ_(i n) sqrt((K_BT)/m) Δt * a`
The temperature inside the air and box are equal to T
At time Δt, the number of air molecules striking to hole inward = `1/2 ρ_(n2) sqrt((K_BT)/m) Δt * a`
Total number of molecules going out from the hole at a time Δt
= `1/2 [ρ_(n1) - ρ_(n2)] sqrt((K_BT)/m) * Δt * a(I)`
Gas equation
`P_1V = μRT`
⇒ `μ = (P_1V)/(RT)`
For box, `μ/V = P_1/(RT)` where μ = number of moles of gas in box
`ρ_(n1) = (N ("Total no. of molecule in box"))/("Volume of box") = (μNA)/V`
= (P_1N_A)/(RT)` per unit volume
Assuming after time T pressure reduced by 0.1 and becomes `(1.5 - 0.1) = 1.4 atm P_2^'`
Thus, the new final density of NA molecule `ρ_(n1)^'`
`ρ_(n1)^' = (P_2N_A)/(RT)` per unit volume (III)
Thus, the total number of molecules going out from volume V
= `(ρ_(n1) - ρ_(n1)^')v`
= `(P_1N_A)/(RT)v - (P^'2N_A)/(RT)v`
= `(N_Av)/(RT) [P_1 - P_2^']` (IV) (From II, III)
`P_2^'` = Net number of molecules going out in time τ from the hole from (I)
= `1/2 [ρ_(n1) - ρ_(n2)] sqrt((K_BT)/m) τ * a`
`ρ_(n1) - ρ_(n2) = (P_1N_A)/(RT) - (P_2N_A)/(RT)`
∴ `ρ_(n1) - ρ_(n2) = N_A/(RT) [P_1 - P_2]` .....(P2 = Press of air out of box)
In τ time the total number of molecules going out from above
= `1/2 N_a/(RT) [P_1 - P_2] sqrt((K_BT)/m) * τ * a`
From (V) and (IV)
`(N_AV)/(RT) (P_1 - P_2^') = 1/2 N_A/(RT) (P_1 - P_2) sqrt((K_BT)/m) * τ * a`
τ = `(N_AV)/(RT) (P_1 - P_2^') (2RT)/N_A 1/((P_1 - P_2)) sqrt(m/(K_BT)) * 1/a`
τ = `(2(P_1 - P_2^'))/((P_1 - P_2)) * V/a sqrt(m/(K_AT))`
= `(2[1.5 - 1.4])/((1.5 - 1)) 1/10^-8 sqrt((46.5 xx 10^-27)/(1.38 xx 10^-23 xx 300))`
= `(2 xx 0.1)/(0.5 xx 10^-8) sqrt((4650 xx 10^(-27+23-2))/(138 xx 3))`
= `0.4 xx 10^+8 sqrt((775 xx 10^-6)/69)`
= `0.4 xx 10^+8 xx 10^-3 x sqrt(11.23)`
= `0.4 xx 10^5 xx 3.35`
τ = `1.34 xx 10^5` sec
APPEARS IN
संबंधित प्रश्न
The figure shows the plot of PV/T versus Pfor 1.00×10–3 kg of oxygen gas at two different temperatures.
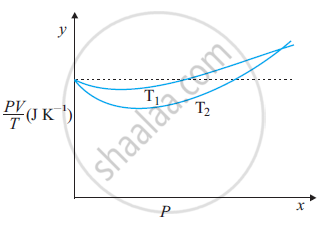
(a) What does the dotted plot signify?
(b) Which is true: T1 > T2 or T1 < T2?
(c) What is the value of PV/T where the curves meet on the y-axis?
(d) If we obtained similar plots for 1.00 ×10–3 kg of hydrogen, would we get the same value of PV/T at the point where the curves meet on the y-axis? If not, what mass of hydrogen yields the same value of PV/T (for low pressure high temperature region of the plot)? (Molecular mass of H2 = 2.02 u, of O2 = 32.0 u, R = 8.31 J mo1–1 K–1.)
Estimate the average thermal energy of a helium atom at the temperature of 10 million Kelvin (the typical core temperature in the case of a star).
Three vessels of equal capacity have gases at the same temperature and pressure. The first vessel contains neon (monatomic), the second contains chlorine (diatomic), and the third contains uranium hexafluoride (polyatomic).
Is the root mean square speed of molecules the same in the three cases? If not, in which case is vrms the largest?
What is diffusion? Give an example to illustrate it.
Name or state the following:
The absolute temperature value corresponding to 35°C.
The average energy per molecule is proportional to ______
Show that for diatomic gas the ratio of the two specific heats is 7:5.
Gases exert pressure on the walls of the container because the gas molecules ______
For a wave, y = 0.0002 sin`[2pi(110"t"-x/3)+pi/3]` is travelling in a medium. The energy per unit volume being transferred by wave if density of medium is 1.5 kg/m3, is ______.
P ∝ T at constant volume is the statement of ______.
