Advertisements
Advertisements
प्रश्न
A box of 1.00 m3 is filled with nitrogen at 1.50 atm at 300K. The box has a hole of an area 0.010 mm2. How much time is required for the pressure to reduce by 0.10 atm, if the pressure outside is 1 atm.
उत्तर
The volume of the box `V_1 = 1 m^3`
Initial pressure `P_1 = 1.5 atm`
Final pressure `P_2^' = 1.5 - 0.1 = 1.4 atm`
Air pressure outside box `P_2 = 1 atm`
Initial temperature `T_1 = 300 K`
Final temperature `T_2 = 300 K`
a = area of hole = 0.01 mm2
= `0.01 xx 10^-6m^2`
= `10^-8m^2`
The initial pressure difference between atmosphere and tyre
`ΔP = (1.5 - 1) atm`
Mass of N2 gas molecule = `(0.028 Kg)/(6.023 xx 10^23)`
= `46.5 xx 10^-27 Kg`
`K_B = 1.38 xx 10^-23`
Assuming `ρ_(i n)` be the initial number of N2 gas molecules per unit volume at time Δt and also `v_(ix)` be the speed of molecules along the x-axis
At time Δt, the number of molecules colliding to the opposite wall
`1/2 ρ_(i n) [(v_(ix)) Δt]A`
Half is multiple as half molecule will strike the opposite wall
`v_(rms)^2 (N_2 "molecules") = v_(ix)^2 + v_(iy)^2 + v_(iz)^2`
∴ `|v_(ix)| = |v_(iy)| = |v_(iz)|`
Thus, `v_(rms)^2 = 3v_(ix)^2`
K.E. of gas molecule = `3/2 K_BT`
`1/2 mv_(rms)^2 = 3/2 K_BT`
`m3v_(ix)^2 = 3K_BT`
`v_(ix) = sqrt((K_BT)/m` .....(A)
At time Δt, the number of N2 gas molecule striking to a wall outward = `1/2 ρ_(i n) sqrt((K_BT)/m) Δt * a`
The temperature inside the air and box are equal to T
At time Δt, the number of air molecules striking to hole inward = `1/2 ρ_(n2) sqrt((K_BT)/m) Δt * a`
Total number of molecules going out from the hole at a time Δt
= `1/2 [ρ_(n1) - ρ_(n2)] sqrt((K_BT)/m) * Δt * a(I)`
Gas equation
`P_1V = μRT`
⇒ `μ = (P_1V)/(RT)`
For box, `μ/V = P_1/(RT)` where μ = number of moles of gas in box
`ρ_(n1) = (N ("Total no. of molecule in box"))/("Volume of box") = (μNA)/V`
= (P_1N_A)/(RT)` per unit volume
Assuming after time T pressure reduced by 0.1 and becomes `(1.5 - 0.1) = 1.4 atm P_2^'`
Thus, the new final density of NA molecule `ρ_(n1)^'`
`ρ_(n1)^' = (P_2N_A)/(RT)` per unit volume (III)
Thus, the total number of molecules going out from volume V
= `(ρ_(n1) - ρ_(n1)^')v`
= `(P_1N_A)/(RT)v - (P^'2N_A)/(RT)v`
= `(N_Av)/(RT) [P_1 - P_2^']` (IV) (From II, III)
`P_2^'` = Net number of molecules going out in time τ from the hole from (I)
= `1/2 [ρ_(n1) - ρ_(n2)] sqrt((K_BT)/m) τ * a`
`ρ_(n1) - ρ_(n2) = (P_1N_A)/(RT) - (P_2N_A)/(RT)`
∴ `ρ_(n1) - ρ_(n2) = N_A/(RT) [P_1 - P_2]` .....(P2 = Press of air out of box)
In τ time the total number of molecules going out from above
= `1/2 N_a/(RT) [P_1 - P_2] sqrt((K_BT)/m) * τ * a`
From (V) and (IV)
`(N_AV)/(RT) (P_1 - P_2^') = 1/2 N_A/(RT) (P_1 - P_2) sqrt((K_BT)/m) * τ * a`
τ = `(N_AV)/(RT) (P_1 - P_2^') (2RT)/N_A 1/((P_1 - P_2)) sqrt(m/(K_BT)) * 1/a`
τ = `(2(P_1 - P_2^'))/((P_1 - P_2)) * V/a sqrt(m/(K_AT))`
= `(2[1.5 - 1.4])/((1.5 - 1)) 1/10^-8 sqrt((46.5 xx 10^-27)/(1.38 xx 10^-23 xx 300))`
= `(2 xx 0.1)/(0.5 xx 10^-8) sqrt((4650 xx 10^(-27+23-2))/(138 xx 3))`
= `0.4 xx 10^+8 sqrt((775 xx 10^-6)/69)`
= `0.4 xx 10^+8 xx 10^-3 x sqrt(11.23)`
= `0.4 xx 10^5 xx 3.35`
τ = `1.34 xx 10^5` sec
APPEARS IN
संबंधित प्रश्न
The figure shows the plot of PV/T versus Pfor 1.00×10–3 kg of oxygen gas at two different temperatures.
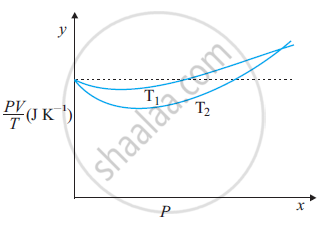
(a) What does the dotted plot signify?
(b) Which is true: T1 > T2 or T1 < T2?
(c) What is the value of PV/T where the curves meet on the y-axis?
(d) If we obtained similar plots for 1.00 ×10–3 kg of hydrogen, would we get the same value of PV/T at the point where the curves meet on the y-axis? If not, what mass of hydrogen yields the same value of PV/T (for low pressure high temperature region of the plot)? (Molecular mass of H2 = 2.02 u, of O2 = 32.0 u, R = 8.31 J mo1–1 K–1.)
50 m3 of saturated vapour is cooled down from 30°C to 20°C. Find the mass of the water condensed. The absolute humidity of saturated water vapour is 30 g m−3 at 30°C and 16 g m−3 at 20°C.
Match the following:
|
|
Column A |
Column B |
|
(a) |
cm3 |
(i) Pressure |
|
(b) |
Kelvin |
(ii) Temperature |
|
(c) |
Torr |
(iii) Volume |
|
(d) |
Boyle's law |
(iv) `"V"/"T" = ("V"_1)/("T"_1)` |
|
(a) |
Charles's law |
(v) `"PV"/"T" = ("P"_1 "V"_1)/"T"_1` |
|
|
|
(vi) PV = P1V1 |
A gas occupies 500 cm3 at a normal temperature. At what temperature will the volume of the gas be reduced by 20% of its original volume, the pressure is constant?
Correct the following statement:
0°C is equal to zero Kelvin.
Name or state the following:
The standard pressure of a gas in cm. of mercury corresponding to one atmospheric pressure.
If the absolute temperature of a body is doubled, the power radiated will increase by a factor of ______
Show that for monoatomic gas the ratio of the two specific heats is 5:3.
Gases exert pressure on the walls of the container because the gas molecules ______
The volume V of an enclosure contains a mixture of three gases, 16 g of oxygen, 28 g of nitrogen and 44 g of carbon dioxide at absolute temperature T. Consider R as universal gas constant. The pressure of the mixture of gases is ______.
