Advertisements
Advertisements
प्रश्न
A car made a run of 390 km in ‘x’ hours. If the speed had been 4 km/hour more, it would have taken 2 hours less for the journey. Find ‘x’.
उत्तर
Let the original speed of the car be y km/hr
We know
`"Speed" = "Distance"/"Time"`
∴ `y = 390/x`
`=> x = 390/y` ...(1)
New speed of the car = (y + 4) km/hr
New time taken by the car to cover 390 km = `390/(y + 4)`
From the given information,
`390/y - 390/(y + 4) = 2`
`(390y + 1560 - 390y)/(y(y + 4)) = 2`
`780/(y^2 + 4y) = 1`
y2 + 4y – 780 = 0
y2 + 30y – 26y – 780 = 0
y(y + 30) – 26(y + 30) = 0
(y + 30)(y – 26) = 0
y = –30, 26
Since, time cannot be negative, so y = 26
From (1), we have
`x = 390/y = 390/26 = 15`
APPEARS IN
संबंधित प्रश्न
The sides of a right-angled triangle containing the right angle are 4x cm and (2x – 1) cm. If the area of the triangle is 30 cm2; calculate the lengths of its sides.
The hypotenuse of a right-angled triangle is 26 cm and the sum of other two sides is 34 cm. Find the lengths of its sides.
The sides of a right-angled triangle are (x – 1) cm, 3x cm and (3x + 1) cm. Find:
- the value of x,
- the lengths of its sides,
- its area.
The hypotenuse of a right-angled triangle exceeds one side by 1 cm and the other side by 18 cm; find the lengths of the sides of the triangle.
The diagonal of a rectangle is 60 m more than its shorter side and the larger side is 30 m more than the shorter side. Find the sides of the rectangle.
Two squares have sides x cm and (x + 4) cm. The sum of their area is 656 sq. cm. Express this as an algebraic equation in x and solve the equation to find the sides of the squares.
A farmer has 70 m of fencing, with which he encloses three sides of a rectangular sheep pen; the fourth side being a wall. If the area of the pen is 600 sq. m, find the length of its shorter side.
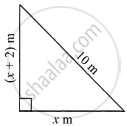
In the given figure, the value of x is ______.
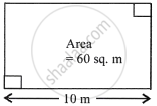
The area of the given rectangle is 60 sq. m and its longer side is 10 m, the perimeter of the rectangle is ______.
The length of a rectangle is 3 m more than its width. If its area is 180 m2; the length of the rectangle is ______.
