Advertisements
Advertisements
Question
A car made a run of 390 km in ‘x’ hours. If the speed had been 4 km/hour more, it would have taken 2 hours less for the journey. Find ‘x’.
Solution
Let the original speed of the car be y km/hr
We know
`"Speed" = "Distance"/"Time"`
∴ `y = 390/x`
`=> x = 390/y` ...(1)
New speed of the car = (y + 4) km/hr
New time taken by the car to cover 390 km = `390/(y + 4)`
From the given information,
`390/y - 390/(y + 4) = 2`
`(390y + 1560 - 390y)/(y(y + 4)) = 2`
`780/(y^2 + 4y) = 1`
y2 + 4y – 780 = 0
y2 + 30y – 26y – 780 = 0
y(y + 30) – 26(y + 30) = 0
(y + 30)(y – 26) = 0
y = –30, 26
Since, time cannot be negative, so y = 26
From (1), we have
`x = 390/y = 390/26 = 15`
APPEARS IN
RELATED QUESTIONS
The sides of a right-angled triangle containing the right angle are 4x cm and (2x – 1) cm. If the area of the triangle is 30 cm2; calculate the lengths of its sides.
The hypotenuse of a right-angled triangle is 26 cm and the sum of other two sides is 34 cm. Find the lengths of its sides.
The hypotenuse of a right-angled triangle exceeds one side by 1 cm and the other side by 18 cm; find the lengths of the sides of the triangle.
The diagonal of a rectangle is 60 m more than its shorter side and the larger side is 30 m more than the shorter side. Find the sides of the rectangle.
Two squares have sides x cm and (x + 4) cm. The sum of their area is 656 sq. cm. Express this as an algebraic equation in x and solve the equation to find the sides of the squares.
The dimensions of a rectangular field are 50 m and 40 m. A flower bed is prepared inside this field leaving a gravel path of uniform width all around the flower bed. The total cost of laying the flower bed and gravelling the path at Rs. 30 and Rs. 20 per square metre, respectively, is Rs. 52,000. Find the width of the gravel path.
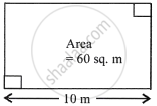
The area of the given rectangle is 60 sq. m and its longer side is 10 m, the perimeter of the rectangle is ______.
The perimeter of a square is numerically equal to its area. The perimeter of the square is ______.
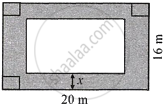
If the width of the uniform shaded portion of x m; its area in terms of x is ______.
The length of a rectangle is 3 m more than its width. If its area is 180 m2; the length of the rectangle is ______.
