Advertisements
Advertisements
Question
The hypotenuse of a right-angled triangle exceeds one side by 1 cm and the other side by 18 cm; find the lengths of the sides of the triangle.
Advertisements
Solution
Let one hypotenuse of the triangle be x cm.
From the given information,
Length of one side = (x – 1) cm
Length of other side = (x – 18) cm
Using Pythagoras theorem,
x2 = (x – 1)2 + (x – 18)2
x2 = x2 + 1 – 2x + x2 + 324 – 36x
x2 – 38x + 325 = 0
x2 – 13x – 25x + 325 = 0
x(x – 13) – 25(x – 13) = 0
(x – 13)(x – 25) = 0
x = 13, 25
When x = 13, x – 18 = 13 – 18 = –5, which being negative, is not possible.
So, x = 25
Thus, the lengths of the sides of the triangle are x = 25 cm, (x – 1) = 24 cm and (x – 18) = 7 cm.
APPEARS IN
RELATED QUESTIONS
The sides of a right-angled triangle containing the right angle are 4x cm and (2x – 1) cm. If the area of the triangle is 30 cm2; calculate the lengths of its sides.
The hypotenuse of a right-angled triangle is 26 cm and the sum of other two sides is 34 cm. Find the lengths of its sides.
A footpath of uniform width runs round the inside of a rectangular field 32 m long and 24 m wide. If the path occupies 208 m2, find the width of the footpath.
Two squares have sides x cm and (x + 4) cm. The sum of their area is 656 sq. cm. Express this as an algebraic equation in x and solve the equation to find the sides of the squares.
An area is paved with square tiles of a certain size and the number required is 128. If the tiles had been 2 cm smaller each way, 200 tiles would have been needed to pave the same area. Find the size of the larger tiles.
A square lawn is bounded on three sides by a path 4 m wide. If the area of the path is `7/8` that of the lawn, find the dimensions of the lawn.
The area of a big rectangular room is 300 m2. If the length were decreased by 5 m and the breadth increased by 5 m; the area would be unaltered. Find the length of the room.
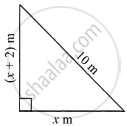
In the given figure, the value of x is ______.
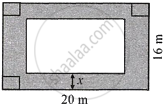
If the width of the uniform shaded portion of x m; its area in terms of x is ______.
The length of a rectangle is 3 m more than its width. If its area is 180 m2; the length of the rectangle is ______.
