Advertisements
Advertisements
Question
The sides of a right-angled triangle are (x – 1) cm, 3x cm and (3x + 1) cm. Find:
- the value of x,
- the lengths of its sides,
- its area.
Solution
Longer side = Hypotenuse = (3x + 1) cm
Lengths of other two sides are (x – 1) cm and 3x cm.
Using Pythagoras theorem,
(3x + 1)2 = (x – 1)2 + (3x)2
9x2 + 1 + 6x = x2 + 1 – 2x + 9x2
x2 – 8x = 0
x(x – 8) = 0
x = 0, 8
But, if x = 0, then one side = 3x = 0, which is not possible.
So, x = 8
Thus, the lengths of the sides of the triangle are (x – 1) cm = 7 cm, 3x cm = 24 cm and (3x + 1) cm = 25 cm.
Area of the triangle = `1/2` × 7 cm × 24 cm = 84 cm2
APPEARS IN
RELATED QUESTIONS
The perimeter of a rectangle is 104 m and its area is 640 m2. Find its length and breadth.
Two squares have sides x cm and (x + 4) cm. The sum of their area is 656 sq. cm. Express this as an algebraic equation in x and solve the equation to find the sides of the squares.
The dimensions of a rectangular field are 50 m and 40 m. A flower bed is prepared inside this field leaving a gravel path of uniform width all around the flower bed. The total cost of laying the flower bed and gravelling the path at Rs. 30 and Rs. 20 per square metre, respectively, is Rs. 52,000. Find the width of the gravel path.
A farmer has 70 m of fencing, with which he encloses three sides of a rectangular sheep pen; the fourth side being a wall. If the area of the pen is 600 sq. m, find the length of its shorter side.
A square lawn is bounded on three sides by a path 4 m wide. If the area of the path is `7/8` that of the lawn, find the dimensions of the lawn.
The area of a big rectangular room is 300 m2. If the length were decreased by 5 m and the breadth increased by 5 m; the area would be unaltered. Find the length of the room.
A car made a run of 390 km in ‘x’ hours. If the speed had been 4 km/hour more, it would have taken 2 hours less for the journey. Find ‘x’.
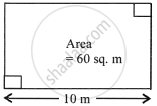
The area of the given rectangle is 60 sq. m and its longer side is 10 m, the perimeter of the rectangle is ______.
The perimeter of a square is numerically equal to its area. The perimeter of the square is ______.
The length of a rectangle is 3 m more than its width. If its area is 180 m2; the length of the rectangle is ______.
