Advertisements
Advertisements
प्रश्न
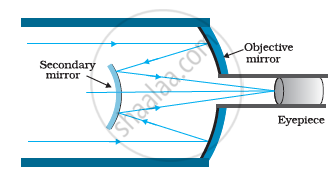
A Cassegrain telescope uses two mirrors as shown in the figure. Such a telescope is built with the mirrors 20 mm apart. If the radius of curvature of the large mirror is 220 mm and the small mirror is 140 mm, where will the final image of an object at infinity be?
उत्तर
A Cassegrain telescope consists of a concave mirror and a convex mirror.
Distance between the objective mirror and the secondary mirror, d = 20 mm
Radius of curvature of the objective mirror, R1 = 220 mm
Hence, focal length of the objective mirror, f1 = `"R"_1/2 = 220/2` = 110 mm
Radius of curvature of the secondary mirror, R2 = 140 mm
Hence, focal length of the secondary mirror, f2 = `"R"_2/2 = 140/2` = 70 mm
The image of an object placed at infinity, formed by the objective mirror, will act as a virtual object for the secondary mirror.
Hence, the virtual object distance for the secondary mirror, u = f1 − d
= 110 − 20
= 90 mm
Applying the mirror formula for the secondary mirror, we can calculate image distance (v) as:
`1/"v" + 1/"u" = 1/"f"_2`
`1/"v" = 1/"f"_2 - 1/"u"`
`1/"v" = 1/70 - 1/90`
`1/"v" = (90 - 70)/6300`
`1/"v" = 20/6300`
`1/"v" = 2/630`
v = `630/2`
∴ v = 315 mm
Hence, the final image will be formed 315 mm away from the secondary mirror.
APPEARS IN
संबंधित प्रश्न
A virtual image, we always say, cannot be caught on a screen. Yet when we ‘see’ a virtual image, we are obviously bringing it on to the ‘screen’ (i.e., the retina) of our eye. Is there a contradiction?
For a normal eye, the far point is at infinity and the near point of distinct vision is about 25cm in front of the eye. The cornea of the eye provides a converging power of about 40 dioptres, and the least converging power of the eye-lens behind the cornea is about 20 dioptres. From this rough data estimate the range of accommodation (i.e., the range of converging power of the eye-lens) of a normal eye.
A myopic person has been using spectacles of power −1.0 dioptre for distant vision. During old age, he also needs to use the separate reading glass of power + 2.0 dioptres. Explain what may have happened.
A person looking at a person wearing a shirt with a pattern comprising vertical and horizontal lines is able to see the vertical lines more distinctly than the horizontal ones. What is this defect due to? How is such a defect of vision corrected?
What should be the distance between the object and the magnifying glass if the virtual image of each square in the figure is to have an area of 6.25 mm2. Would you be able to see the squares distinctly with your eyes very close to the magnifier?
The angle subtended at the eye by an object is equal to the angle subtended at the eye by the virtual image produced by a magnifying glass. In what sense then does a magnifying glass provide angular magnification?
The muscles of a normal eye are least strained when the eye is focussed on an object
A person A can clearly see objects between 25 cm and 200 cm. Which of the following may represent the range of clear vision for a person B having muscles stronger than A, but all other parameters of eye identical to that of A?
The focal length of a normal eye-lens is about
The distance of the eye-lens from the retina is x. For a normal eye, the maximum focal length of the eye-lens
A man wearing glasses of focal length +1 m cannot clearly see beyond 1 m
Mark the correct options.
(a) If the far point goes ahead, the power of the divergent lens should be reduced.
(b) If the near point goes ahead, the power of the convergent lens should be reduced.
(c) If the far point is 1 m away from the eye, divergent lens should be used.
(d) If the near point is 1 m away from the eye, divergent lens should be used.
A person looks at different trees in an open space with the following details. Arrange the trees in decreasing order of their apparent sizes.
| Tree | Height(m) | Distance from the eye(m) |
| A | 2.0 | 50 |
| B | 2.5 | 80 |
| C | 1.8 | 70 |
| D | 2.8 | 100 |
Can virtual image be formed on the retina in a seeing process?
A normal eye has retina 2 cm behind the eye-lens. What is the power of the eye-lens when the eye is (a) fully relaxed, (b) most strained?
