Advertisements
Advertisements
प्रश्न
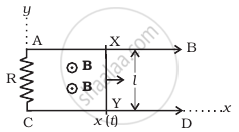
A conducting wire XY of mass m and neglibile resistance slides smoothly on two parallel conducting wires as shown in figure. The closed circuit has a resistance R due to AC. AB and CD are perfect conductors. There is a ˆ. magnetic field `B = B(t)hatk`.
- Write down equation for the acceleration of the wire XY.
- If B is independent of time, obtain v(t) , assuming v(0) = u0.
- For (b), show that the decrease in kinetic energy of XY equals the heat lost in R.
उत्तर
First we have to analyse the situation as shown in the figure. Let the parallel wires be at y = 0 and y = L and are placed along x-axis. Wire XY is along y-axis.
At t = 0, wire AB starts from x = 0 and moves with a velocity v.
Let at time t, wire is at x(t) = vt. ....(Where x(t) is the displacement as a function of time).
Let us redraw the diagram as shown below.
(i) Let wire XY at t = 0 is at x = 0
And at t = t is at x = x(t)
Magnetic flux is a function of time `phi(t) = B(t) xx A`
∴ `phi(t) = B(t)l.x(t)`
`ε = - (dphi(t))/(dt) = - (dB(t))/(dt)l.x(t) - B(t)l. (dx(t))/(dt)`
`ε = (- dB(t))/(dt) l.x(t) - B(t)lv(t)`
The direction of induced current by Fleming's Right-Hand Rule or by Lenz's law is in clockwise direction in loop XY < AX.
`I = ε/R = (-l)/R [x(t) (dB(t))/(dt) + B(t)v(t)]` ......(I)
The force acting on the conductor is F = B(t) I l sin 90°
F = B(t)I.l
F = `(B(t)lε)/R = (-B(t)l^2)/R [(-dB(t))/(dt).x(t) - B(t).v(t)]`
`(md^2x)/(dt^2) = (-B(t)l^2)/R [x(t) (dB(t))/(dt) + B(t)v(t)]`
Or `(d^2x)/(dt^2) = (-l^2)/(mR) B(t) [x(t) (dB(t))/(dt) + B(t).v(t)]` ......(II)
(ii) Now B is independent of time i.e. B does not change with time or it is constant
∴ `(dB)/(dt)` = 0, B(t) = B and v(t) = c ......(III)
Put (III) in (II) we get
`(d^2x)/(dt^2) = (-l^2)/(mR) [0 + Bv]`
`(d^2x)/(dt^2) + (B^2l^2)/(mR) (dx)/(dt)` = 0
`(dv)/(dt) + (B^2l^2)/(mR) v` = 0
Integrating using variable separable from differential equation we have
`v = A exp((-l^2B^2t)/(mR))`
At t = 0, v = u
∴ `v(t) = u exp ((-l^2B^2t)/(mR))` ......(IV)
(iii) Heat lost per second in (ii) where `(dB)/(dt)` = 0
H = I2R
Magnitude of current from equation I in (i) part
`I = (Blv)/R = (-l)/R [0 + Bv]` ......`[because (dB)/(dt) = 0]`
Heat produced per second H = I2R
∴ `H = (B^2l^2v^2)/R^2 R`
`H = (B^2l^2)/R u^2 exp (-2i^2B^2t)/(mR)`
v from equation (IV) in (iii) part
Power lost = `int_0^t I^2 Rdt = (B^2l^2u^2)/R int_0^t e^((-2l^2B^2t)/(mR)) dt` ....`[because v^2 = u^2 exp ^((-2l^2B^2t)/(mR))]`
Power lost = `(B^2l^2u^2)/R (mR)/(2l^2B^2) [1 - e^((-2l^2B^2t)/(mR))]`
= `(m u^2)/2 [1 - e^((-2l^2B^2t)/(mR))]`
= `(m u^2)/2 - m/2 u^2e^((-2l^2B^2t)/(mR))`
= `[(m u^2)/2 - (mv^2(t))/2]`
= initial K.E. – final K.E.
Power lost = decrease in kinetic energy
This proves that decrease in K.E of XY is equal to the heat lost in R.
APPEARS IN
संबंधित प्रश्न
Describe a simple experiment (or activity) to show that the polarity of emf induced in a coil is always such that it tends to produce a current which opposes the change of magnetic flux that produces it.
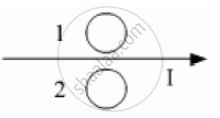
Predict the directions of induced currents in metal rings 1 and 2 lying in the same plane where current I in the wire is increasing steadily.
Predict the direction of induced current in a metal ring when the ring is moved towards a straight conductor with constant speed v. The conductor is carrying current I in the direction shown in the figure.
A bar magnet is released from rest along the axis of a very long, vertical copper tube. After some time the magnet ____________ .
For a coil having L = 2 mH, current flows at the rate of 10-3 AIS. The e.m.f induced is
A wire in the form of a tightly wound solenoid is connected to a DC source, and carries a current. If the coil is stretched so that there are gaps between successive elements of the spiral coil, will the current increase or decrease? Explain.
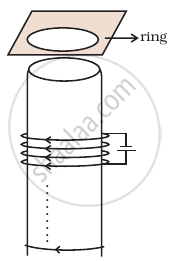
Consider a metal ring kept on top of a fixed solenoid (say on a carboard) (Figure). The centre of the ring coincides with the axis of the solenoid. If the current is suddenly switched on, the metal ring jumps up. Explain
Predict the direction of induced current in the situation described by the following figure.
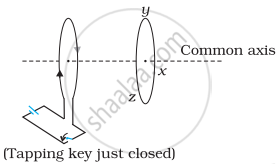
Predict the direction of induced current in the situation described by the following figure.
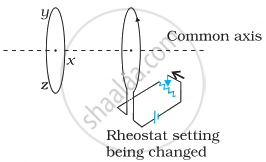
Use Lenz’s law to determine the direction of induced current in the situation described by the figure.
A circular loop being deformed into a narrow straight wire.