Advertisements
Advertisements
प्रश्न
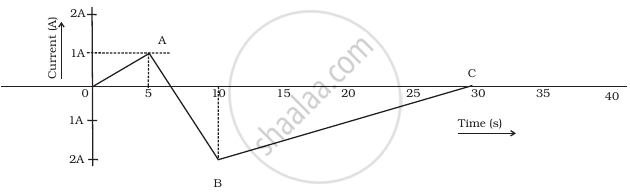
A (current vs time) graph of the current passing through a solenoid is shown in figure. For which time is the back electromotive force (u) a maximum. If the back emf at t = 3s is e, find the back emf at t = 7s, 15s and 40s. OA, AB and BC are straight line segments.
उत्तर
Whenever the electric current passing through a coil or circuit changes, the magnetic flux linked with it will also change. As a result of this, in accordance with Farraday's laws of electromagnetic induction, an emf is induced in the coil or the circuit which opposes the change that causes this induced emf is called back emf, the current so produced in the coil is called induced current. The induced emf is given by
`ε = - (d(Nphi_B))/(dt)`
`ε = - L (dl)/(dt)`
Thus, negative sign indicates that induced emf (e) opposes any change (increase or decrease) of current in the coil.
When the rate of change of current is maximum, then back emf in the solenoid is (u) a maximum. This occurs in AB part of the graph. So maximum back emf will be obtained between 5s < t < 10s.
Since, the back emf at t = 3s is e.
Also, the rate of change of current at t = 3
And slope(s) of OA (from t = 0s to t = 5s) = 1/5 A/s
So, we have
If u = L 1/5 (for t = 3s, `(dI)/(dt)` = 1/5)
Where L is a constant (coefficient of self-induction)
And emf is ε = `- L (dI)/(dt)`
Similarly, we have for other values
For 5s < t < 10s, u1 = `- L 3/5 = - 3/5 L = - 3e`
Thus, at t = 7s, u1 = – 3e
For 10s < t < 30s
u2 = `L 2/20 = L/10 = 1/2 e`
For t > 30s, u2 = 0
Thus, the back emf at t = 7s, 15s and 40s are – 3e e/2 and 0 respectively.
APPEARS IN
संबंधित प्रश्न
A circular coil of radius 8.0 cm and 20 turns is rotated about its vertical diameter with an angular speed of 50 rad s−1 in a uniform horizontal magnetic field of magnitude 3.0 × 10−2 T. Obtain the maximum and average emf induced in the coil. If the coil forms a closed loop of resistance 10 Ω, calculate the maximum value of current in the coil. Calculate the average power loss due to Joule heating. Where does this power come from?
State Faraday's first law of electrolysis.
A 0⋅5 m long solenoid of 10 turns/cm has the area of cross-section 1 cm2. Calculate the voltage induced across its ends if the current in the solenoid is changed from 1 A to A in 0⋅1 s.
Faraday’s laws are consequence of the conservation of ______.
According to Faraday's law of electromagnetic induction, ______
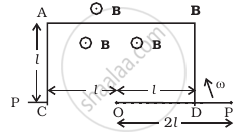
ODBAC is a fixed rectangular conductor of negilible resistance (CO is not connnected) and OP is a conductor which rotates clockwise with an angular velocity ω (Figure). The entire system is in a uniform magnetic field B whose direction is along the normal to the surface of the rectangular conductor ABDC. The conductor OP is in electric contact with ABDC. The rotating conductor has a resistance of λ per unit length. Find the current in the rotating conductor, as it rotates by 180°.
A magnetic field B is confined to a region r ≤ a and points out of the paper (the z-axis), r = 0 being the centre of the circular region. A charged ring (charge = Q) of radius b, b > a and mass m lies in the x-y plane with its centre at the origin. The ring is free to rotate and is at rest. The magnetic field is brought to zero in time ∆t. Find the angular velocity ω of the ring after the field vanishes.
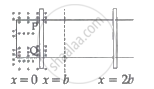
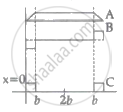
The arm PQ of a rectangular conductor is moving from x = 0 to x = 2b outwards and then inwards from x = 2b to x = 0 as shown in the figure. A uniform magnetic field perpendicular to the plane is acting from x = 0 to x = b. Identify the graph showing the variation of different quantities with distance.
Two coils C1 and C2 are placed close to each other. The magnetic flux Φ2 linked with coil C2 varies with the current I1 flowing in coil C1 as shown in the figure. Find
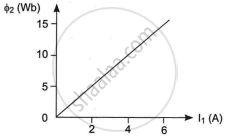
- The mutual inductance of the arrangement, and
- The rate of change of current `((dI_1)/(dt))` will induce an emf of 100V in coil C2.
