Advertisements
Advertisements
प्रश्न
Find the current in the wire for the configuration shown in figure. Wire PQ has negligible resistance. B, the magnetic field is coming out of the paper. θ is a fixed angle made by PQ travelling smoothly over two conducting parallel wires separated by a distance d.
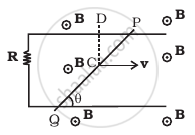
उत्तर
This problem is based upon the motional emf. Consider a conducting rod of length l moving with a uniform velocity v perpendicular to a uniform magnetic field B bar, directed into the plane of the paper. Let the rod be moving to the right as shown in figure. The conducting electrons also move to the right as they are trapped within the rod.
Conducting electrons experience a magnetic force Fm = evB. So they move from P to Q within the rod. The end P of the rod becomes positively charged while end Q becomes negatively charged, hence an electric field is set up within the rod which opposes the further downward movement of electrons, i.e., an equilibrium is reached and in equilibrium Fe = Fm, i.e., eE = evB or R = vB ⇒ Inducted emf e = `El = Bwl [E = V/l]`
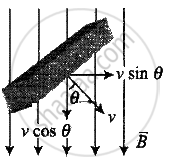
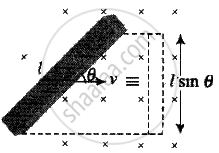
If rod is moved by making an angle θ with the direction of magnetic field or length. Induced emf, `e = Bvl sin θ`
 (A) |
 (B) |
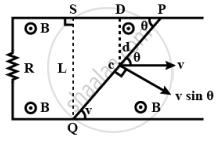
Emf induced across PQ due to its motion or change in magnetic flux linked with the loop change due to the change of enclosed area.
The induced electric field E along the dotted line CD (Perpendicular to both `vecv` and `vecB` along `vecv xx vecB`) = `vB`
Therefore, the emotional emf along
PQ = (length PQ) × (field along PQ)
= (length PQ) × (vB sin θ)
= `(d/sin theta) xx (vB sin theta) = vBd`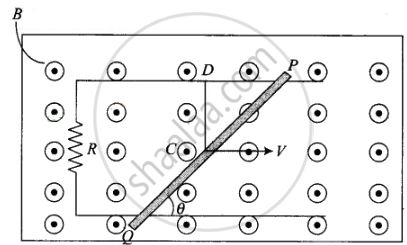
This induced emf make flow of current in closed circuit of resistance R.
`I = (dvB)/R` and is independent of θ.
APPEARS IN
संबंधित प्रश्न
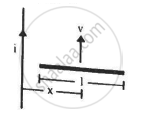
Figure shows a straight, long wire carrying a current i and a rod of length l coplanar with the wire and perpendicular to it. The rod moves with a constant velocity v in a direction parallel to the wire. The distance of the wire from the centre of the rod is x. Find the motional emf induced in the rod.
An aircraft of wing span of 50 m flies horizontally in the Earth's magnetic field of 6 x 10-5 T at a speed of 400 m/s. Calculate the emf generated between the tips of the wings of the aircraft.
A metal disc of radius 30 cm spins at 20 revolution per second about its transverse symmetry axis in a uniform magnetic field of 0.20 T. The field is parallel to the axis of rotation. Calculate
(a) the area swept out per second by the radius of the disc
(b) the flux cut per second by a radius of the disc
(c) the induced emf between the axle and rim of the disc.
The emf induced across the ends of a conductor due to its motion in a magnetic field is called motional emf. It is produced due to magnetic Lorentz force acting on the free electrons of the conductor. For a circuit shown in the figure, if a conductor of length l moves with velocity v in a magnetic field B perpendicular to both its length and the direction of the magnetic field, then all the induced parameters are possible in the circuit.
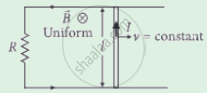
A conducting rod of length l is moving in a transverse magnetic field of strength B with velocity v. The resistance of the rod is R. The current in the rod is ______.
Motional e.m.f is the induced e.m.f. ______
A circular coil expands radially in a region of magnetic field and no electromotive force is produced in the coil. This can be because ______.
- the magnetic field is constant.
- the magnetic field is in the same plane as the circular coil and it may or may not vary.
- the magnetic field has a perpendicular (to the plane of the coil) component whose magnitude is decreasing suitably.
- there is a constant magnetic field in the perpendicular (to the plane of the coil) direction.
A magnetic field B = Bo sin ( ωt )`hatk` wire AB slides smoothly over two parallel conductors separated by a distance d (Figure). The wires are in the x-y plane. The wire AB (of length d) has resistance R and the parallel wires have negligible resistance. If AB is moving with velocity v, what is the current in the circuit. What is the force needed to keep the wire moving at constant velocity?
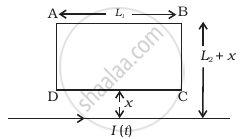
A rectangular loop of wire ABCD is kept close to an infinitely long wire carrying a current I(t) = Io (1 – t/T) for 0 ≤ t ≤ T and I(0) = 0 for t > T (Figure). Find the total charge passing through a given point in the loop, in time T. The resistance of the loop is R.
A rod of mass m and resistance R slides smoothly over two parallel perfectly conducting wires kept sloping at an angle θ with respect to the horizontal (Figure). The circuit is closed through a perfect conductor at the top. There is a constant magnetic field B along the vertical direction. If the rod is initially at rest, find the velocity of the rod as a function of time.

An aircraft of wing span of 60 m flies horizontally in earth’s magnetic field of 6 × 10−5 T at a speed of 500 m/s. Calculate the e.m.f. induced between the tips of the wings of the aircraft.
