Advertisements
Advertisements
प्रश्न
A rod of mass m and resistance R slides smoothly over two parallel perfectly conducting wires kept sloping at an angle θ with respect to the horizontal (Figure). The circuit is closed through a perfect conductor at the top. There is a constant magnetic field B along the vertical direction. If the rod is initially at rest, find the velocity of the rod as a function of time.

उत्तर
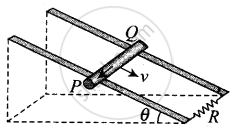
Let us first divide the magnetic field in the components one is along the inclined plane = B sin θ and other component of magnetic field is perpendicular the plane = B cos θ
Now, the conductor moves with speed v perpendicular to B cos θ, component of magnetic field. This causes motional emf across two ends of rod, which is given by = v(B cos θ)d
 (A) |
 (B) |
This makes flow of induced current `i = (v(B cos theta)d)/R` where R is the resistance of rod. Now, current carrying rod experience a magnetic force which is given by `F_m = iBd` (horizontally in backwards direction). Now, the component of magnetic force parallel to the inclined plane in upward direction
`F_(||) = F_m cos θ = -Bd cos θ = ((v(B cos θ)d)/R) Bd cos θ`
Where, `v = (dx)/(dt)`
Also, the component of weight (mg) parallel to the inclined plane along downward direction = mg sin θ.
Now, by Newton's second law of motion
`m (d^2x)/(dl^2) = mg sin θ - (B cos θ d)/R ((dx)/(dt)) xx (Bd) cos θ`
⇒ `(dv)/(dt) = g sin θ - (B^2d^2)/(mR) (cos theta)^2v`
⇒ `(dv)/(dt) + (B^2d^2)/(mR) (cos θ)^2v = g sin θ`
But, this is the linear differential equation.
On solving, we get
`v = ((g sin θ)/(B^2d^2 cos^2 θ))/(mR) + A exp(- (B^2d^2)/(mR) (cos^2 θ)t)`
A is a constant to be determined by initial conditions.
The required expression of velocity as a function of time is given by
= `(mgR sin θ)/(B^2d^2 cos^2θ) (1 - exp (- (B^2d^2)/(mR) (cos^2θ)t))`
APPEARS IN
संबंधित प्रश्न
A conducting disc of radius r rotates with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
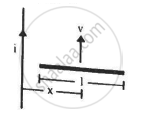
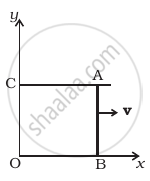
Figure shows a straight, long wire carrying a current i and a rod of length l coplanar with the wire and perpendicular to it. The rod moves with a constant velocity v in a direction parallel to the wire. The distance of the wire from the centre of the rod is x. Find the motional emf induced in the rod.
The emf induced across the ends of a conductor due to its motion in a magnetic field is called motional emf. It is produced due to magnetic Lorentz force acting on the free electrons of the conductor. For a circuit shown in the figure, if a conductor of length l moves with velocity v in a magnetic field B perpendicular to both its length and the direction of the magnetic field, then all the induced parameters are possible in the circuit.
Direction of current induced in a wire moving in a magnetic field is found using ______.
The emf induced across the ends of a conductor due to its motion in a magnetic field is called motional emf. It is produced due to magnetic Lorentz force acting on the free electrons of the conductor. For a circuit shown in the figure, if a conductor of length l moves with velocity v in a magnetic field B perpendicular to both its length and the direction of the magnetic field, then all the induced parameters are possible in the circuit.
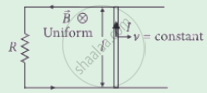
A 0.1 m long conductor carrying a current of 50 A is held perpendicular to a magnetic field of 1.25 mT. The mechanical power required to move the conductor with a speed of 1 ms-1 is ______.
A circular coil expands radially in a region of magnetic field and no electromotive force is produced in the coil. This can be because ______.
- the magnetic field is constant.
- the magnetic field is in the same plane as the circular coil and it may or may not vary.
- the magnetic field has a perpendicular (to the plane of the coil) component whose magnitude is decreasing suitably.
- there is a constant magnetic field in the perpendicular (to the plane of the coil) direction.
A magnetic field B = Bo sin ( ωt )`hatk` wire AB slides smoothly over two parallel conductors separated by a distance d (Figure). The wires are in the x-y plane. The wire AB (of length d) has resistance R and the parallel wires have negligible resistance. If AB is moving with velocity v, what is the current in the circuit. What is the force needed to keep the wire moving at constant velocity?
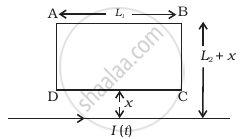
A rectangular loop of wire ABCD is kept close to an infinitely long wire carrying a current I(t) = Io (1 – t/T) for 0 ≤ t ≤ T and I(0) = 0 for t > T (Figure). Find the total charge passing through a given point in the loop, in time T. The resistance of the loop is R.
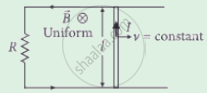
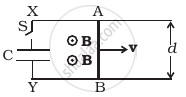
Find the current in the sliding rod AB (resistance = R) for the arrangement shown in figure. B is constant and is out of the paper. Parallel wires have no resistance. v is constant. Switch S is closed at time t = 0.
An aeroplane, with its wings spread 10 m, is flying at a speed of 180 km/h in a horizontal direction. The total intensity of earth's field at that part is 2.5 × 10-4 Wb/m2 and the angle of dip is 60°. The emf induced between the tips of the plane wings will be ______.
A wire 5 m long is supported horizontally at a height of 15 m along an east-west direction. When it is about to hit the ground, calculate the average e.m.f. induced in it. (g = 10 m/s2)
