Advertisements
Advertisements
प्रश्न
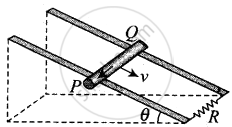
A rod of mass m and resistance R slides smoothly over two parallel perfectly conducting wires kept sloping at an angle θ with respect to the horizontal (Figure). The circuit is closed through a perfect conductor at the top. There is a constant magnetic field B along the vertical direction. If the rod is initially at rest, find the velocity of the rod as a function of time.

उत्तर
Let us first divide the magnetic field in the components one is along the inclined plane = B sin θ and other component of magnetic field is perpendicular the plane = B cos θ
Now, the conductor moves with speed v perpendicular to B cos θ, component of magnetic field. This causes motional emf across two ends of rod, which is given by = v(B cos θ)d
 (A) |
 (B) |
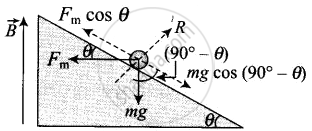
This makes flow of induced current `i = (v(B cos theta)d)/R` where R is the resistance of rod. Now, current carrying rod experience a magnetic force which is given by `F_m = iBd` (horizontally in backwards direction). Now, the component of magnetic force parallel to the inclined plane in upward direction
`F_(||) = F_m cos θ = -Bd cos θ = ((v(B cos θ)d)/R) Bd cos θ`
Where, `v = (dx)/(dt)`
Also, the component of weight (mg) parallel to the inclined plane along downward direction = mg sin θ.
Now, by Newton's second law of motion
`m (d^2x)/(dl^2) = mg sin θ - (B cos θ d)/R ((dx)/(dt)) xx (Bd) cos θ`
⇒ `(dv)/(dt) = g sin θ - (B^2d^2)/(mR) (cos theta)^2v`
⇒ `(dv)/(dt) + (B^2d^2)/(mR) (cos θ)^2v = g sin θ`
But, this is the linear differential equation.
On solving, we get
`v = ((g sin θ)/(B^2d^2 cos^2 θ))/(mR) + A exp(- (B^2d^2)/(mR) (cos^2 θ)t)`
A is a constant to be determined by initial conditions.
The required expression of velocity as a function of time is given by
= `(mgR sin θ)/(B^2d^2 cos^2θ) (1 - exp (- (B^2d^2)/(mR) (cos^2θ)t))`
APPEARS IN
संबंधित प्रश्न
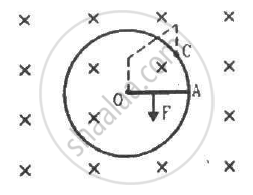
Consider the situation shown in the figure. Suppose the wire connecting O and C has zero resistance but the circular loop has a resistance Runiformly distributed along its length. The rod OA is made to rotate with a uniform angular speed ω as shown in the figure. Find the current in the rod when ∠ AOC = 90°.
An aircraft of wing span of 50 m flies horizontally in the Earth's magnetic field of 6 x 10-5 T at a speed of 400 m/s. Calculate the emf generated between the tips of the wings of the aircraft.
A cycle wheel of radius 0.6 m is rotated with constant angular velocity of 15 rad/s in a region of magnetic field of 0.2 T which is perpendicular to the plane of the wheel. The e.m.f generated between its center and the rim is, ____________.
A conducting square loop of side l and resistance R moves in its plane with a uniform velocity v perpendicular to one of its side. A magnetic induction B constant in time and space, pointing perpendicular and into the plane of the loop exists everywhere. The current induced in the loop is ______.
A wire of length 50 cm moves with a velocity of 300 m/min, perpendicular to a magnetic field. If the e.m.f. induced in the wire is 2 V, the magnitude of the field in tesla is ______.
The emf induced across the ends of a conductor due to its motion in a magnetic field is called motional emf. It is produced due to magnetic Lorentz force acting on the free electrons of the conductor. For a circuit shown in the figure, if a conductor of length l moves with velocity v in a magnetic field B perpendicular to both its length and the direction of the magnetic field, then all the induced parameters are possible in the circuit.
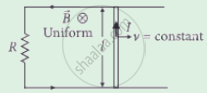
A conducting rod of length l is moving in a transverse magnetic field of strength B with velocity v. The resistance of the rod is R. The current in the rod is ______.
The emf induced across the ends of a conductor due to its motion in a magnetic field is called motional emf. It is produced due to magnetic Lorentz force acting on the free electrons of the conductor. For a circuit shown in the figure, if a conductor of length l moves with velocity v in a magnetic field B perpendicular to both its length and the direction of the magnetic field, then all the induced parameters are possible in the circuit.
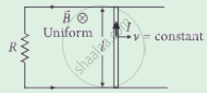
A 0.1 m long conductor carrying a current of 50 A is held perpendicular to a magnetic field of 1.25 mT. The mechanical power required to move the conductor with a speed of 1 ms-1 is ______.
An aeroplane, with its wings spread 10 m, is flying at a speed of 180 km/h in a horizontal direction. The total intensity of earth's field at that part is 2.5 × 10-4 Wb/m2 and the angle of dip is 60°. The emf induced between the tips of the plane wings will be ______.
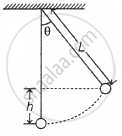
A simple pendulum with a bob of mass m and conducting wire of length L swings under gravity through an angle θ. The component of the earth's magnetic field in the direction perpendicular to the swing is B. Maximum emf induced across the pendulum is ______.
(g = acceleration due to gravity)
Derive an expression for the total emf induced in a conducting rotating rod.
