Advertisements
Advertisements
प्रश्न
A four-digit number abcd is divisible by 11, if d + b = ______ or _____.
उत्तर
A four-digit number abcd is divisible by 11, if d + b = a + c or 12(a + c).
Explanation:
We know that, a number is divisible by 11, if the difference between the sum of digits at odd places and the sum of its digits at even places is either 0 or a multiple of 11.
Hence, abcd is divisible by 11, if (d + b) – (a + c) = 0, 11, 22, 33, ...
⇒ d + b = a + c or d + b = 12(a + c)
APPEARS IN
संबंधित प्रश्न
Given an example of a number which is divisible by 2 but not by 4.
Given an example of a number which is divisible by both 4 and 8 but not by 32.
Which of the following statement is true?
A number is divisible by 18, if it is divisible by both 3 and 6.
Do you remember magic triangles? Come now, let s make some magic squares.
- Fill this square using all the numbers from 21 to 29.
Rule: The total of each side is 75.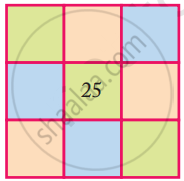
Look at the patterns of numbers in hexagons.
Each side has 2 circles and 1 box.
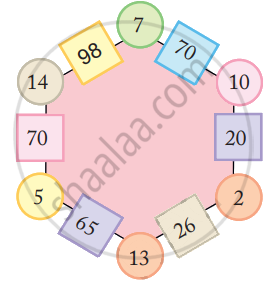
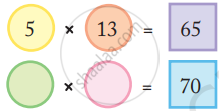
- Look at the number 65 in the box. Which are the circles next to it?
- Can you see how the rule works?
Now you try and change these numbers into special numbers —
273
Find the least value that must be given to number a so that the number 91876a2 is divisible by 8.
A five-digit number AABAA is divisible by 33. Write all the numbers of this form.
If 148101B095 is divisible by 33, find the value of B.
Fill in the blank space in the same way.

