Advertisements
Advertisements
Question
A four-digit number abcd is divisible by 11, if d + b = ______ or _____.
Solution
A four-digit number abcd is divisible by 11, if d + b = a + c or 12(a + c).
Explanation:
We know that, a number is divisible by 11, if the difference between the sum of digits at odd places and the sum of its digits at even places is either 0 or a multiple of 11.
Hence, abcd is divisible by 11, if (d + b) – (a + c) = 0, 11, 22, 33, ...
⇒ d + b = a + c or d + b = 12(a + c)
APPEARS IN
RELATED QUESTIONS
Given an example of a number which is divisible by 3 but not by 6.
Which of the following statement is true?
If a number divides three numbers exactly, it must divide their sum exactly.
Look at the patterns of numbers in hexagons.
Each side has 2 circles and 1 box.
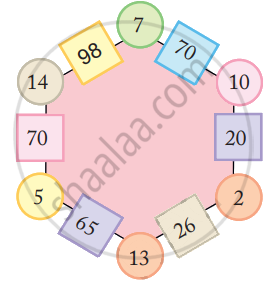
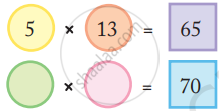
- Look at the number 65 in the box. Which are the circles next to it?
- Can you see how the rule works?
Use the same rule to fill the hexagons below.
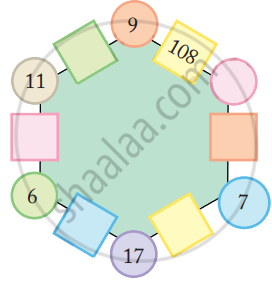
Now you also make your own magic hexagons.
Fill in the blank space in the same way.
If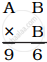 
then A = ______ and B = ______.
If B × B = AB, then either A = 2, B = 5 or A = ______, B = ______.
A four-digit number abcd is divisible by 4 if ab is divisible by 4.
756x is a multiple of 11, find the value of x.
If 123123A4 is divisible by 11, find the value of A.
