Advertisements
Advertisements
प्रश्न
A function f is defined as follows:
`f(x) = {{:(0, "for" x < 0;),(x, "for" 0 ≤ x ≤ 1;),(- x^2 +4x - 2, "for" 1 ≤ x ≤ 3;),(4 - x, "for" x ≥ 3):}`
Is the function continuous?
उत्तर
`f(x) = {{:(0, "for" x < 0),(x, "for" 0 ≤ x ≤ 1),(- x^2 +4x - 2, "for" 1 ≤ x ≤ 3),(4 - x, "for" x ≥ 3):}`
`lim_(x -> 0^-) f(x) = lim_(x -> 0^-) 0` = 0
`lim_(x -> 0^+) f(x) = lim_(x -> 0^+) x` = 0
∴ `lim_(x -> 0-) f(x) = lim_(x -> 0^+) f(x)` = 0
Hence `lim_(x -> 0) f(x)` = 0 .......(1)
`f(0)` = 0 .......(2)
From equations (1) and (2) we get
`lim_(x -> 0) f(x) = f(0)`
∴ f(x) is continuos at x = 0.
`lim_(x -> 1^-) f(x) = lim_(x -> 1^-) x` = 1
`lim_(x -> 1^-) f(x) = lim_(x -> 1^+) ( x^2 + 4x - 2)`
= – 12 – 4 × 1 – 2
= – 1 + 4 – 2
= 4 – 3
= 1
`lim_(x -> 1^-) f(x)` = 1
∴ `lim_(x -> 1) f(x) = lim_(x -> 1^+) f(x)` = 1
Hence `lim_(x -> 1) f(x)` = 1 ........(3)
`f(1) = -1^2 + 4 xx 1 - 2`
= `-1 + 4 - 2`
`f(1)` = 4 – 3
= 1 ........(4)
Fom equaton (3) and (4) we have
`lim_(x -> 1) f(x) = f(1)`
∴ f(x) is continuos at x = 1.
`lim_(x -> 3^-) f(x) = lim_(x -> 3^-) (- x^2 + 4x - 2)`
= `- 3^2 + 4 xx 3 - 2`
= `- 9 + 12 - 2`
= `- 11 + 12`
= 1
`lim_(x -> 3^-) f(x)` = 1
`lim_(x -> 3^+) f(x) = lim_(x -> 3^+) (4 - x)`
`lim_(x -> 3^+) f(x)` = 4 – 3
= 1
APPEARS IN
संबंधित प्रश्न
Prove that f(x) = 2x2 + 3x - 5 is continuous at all points in R
Find the points of discontinuity of the function f, where `f(x) = {{:(4x + 5",", "if", x ≤ 3),(4x - 5",", "if", x > 3):}`
Find the points of discontinuity of the function f, where `f(x) = {{:(x + 2",", "if", x ≥ 2),(x^2",", "if", x < 2):}`
At the given point x0 discover whether the given function is continuous or discontinuous citing the reasons for your answer:
x0 = 3, `f(x) = {{:((x^2 - 9)/(x - 3)",", "if" x ≠ 3),(5",", "if" x = 3):}`
If f and g are continuous functions with f(3) = 5 and `lim_(x -> 3) [2f(x) - g(x)]` = 4, find g(3)
Find the points at which f is discontinuous. At which of these points f is continuous from the right, from the left, or neither? Sketch the graph of f.
`f(x) = {{:(2x + 1",", "if" x ≤ - 1),(3x",", "if" - 1 < x < 1),(2x - 1",", "if" x ≥ 1):}`
Find the points at which f is discontinuous. At which of these points f is continuous from the right, from the left, or neither? Sketch the graph of f.
`f(x) = {{:((x - 1)^3",", "if" x < 0),((x + 1)^3",", "if" x ≥ 0):}`
Which of the following functions f has a removable discontinuity at x = x0? If the discontinuity is removable, find a function g that agrees with f for x ≠ x0 and is continuous on R.
`f(x) = (x^2 - 2x - 8)/(x + 2), x_0` = – 2
The function `f(x) = (x^2 - 1)/(x^3 - 1)` is not defined at x = 1. What value must we give f(1) inorder to make f(x) continuous at x =1?
State how continuity is destroyed at x = x0 for the following graphs.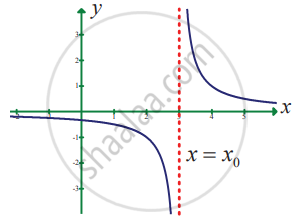
Choose the correct alternative:
If f : R → R is defined by `f(x) = [x - 3] + |x - 4|` for x ∈ R then `lim_(x -> 3^-) f(x)` is equal to
Choose the correct alternative:
The value of `lim_(x -> "k") x - [x]`, where k is an integer is
Choose the correct alternative:
At x = `3/2` the function f(x) = `|2x - 3|/(2x - 3)` is
Choose the correct alternative:
Let f : R → R be defined by `f(x) = {{:(x, x "is irrational"),(1 - x, x "is rational"):}` then f is
Choose the correct alternative:
Let f be a continuous function on [2, 5]. If f takes only rational values for all x and f(3) = 12, then f(4.5) is equal to
Choose the correct alternative:
Let a function f be defined by `f(x) = (x - |x|)/x` for x ≠ 0 and f(0) = 2. Then f is
