Advertisements
Advertisements
प्रश्न
A hemispherical tank is made up of an iron sheet 1 cm thick. If the inner radius is 1 m, then find the volume of the iron used to make the tank.
`["Assume "pi=22/7]`
उत्तर
Inner radius (r1) of hemispherical tank = 1 m
Thickness of hemispherical tank = 1 cm = 0.01 m
Outer radius (r2) of hemispherical tank = (1 + 0.01) m = 1.01 m
The volume of iron used to make such a tank = `2/3pi (r_2^3-r_1^3)`
= `[2/3xx22/7xx{(1.01)^3-(1)^3}]m^3`
= `[44/21xx(1.030301-1)]m^3`
= 0.06348 m3 (approximately)
APPEARS IN
संबंधित प्रश्न
Find the volume of a sphere whose radius is 7 cm.
`["Assume "pi=22/7]`
Find the volume of a sphere whose radius is 0.63 m.
`["Assume "pi=22/7]`
A capsule of medicine is in the shape of a sphere of diameter 3.5 mm. How much medicine (in mm3) is needed to fill this capsule?
`["Assume "pi=22/7]`
The diameter of the moon is approximately one-fourth of the diameter of the earth. What fraction of the volume of the earth is the volume of the moon?
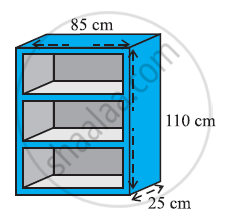
A wooden bookshelf has external dimensions as follows: Height = 110 cm, Depth = 25 cm, Breadth = 85 cm (see the given figure). The thickness of the plank is 5 cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is 20 paise per cm2 and the rate of painting is 10 paise per cm2, find the total expenses required for polishing and painting the surface of the bookshelf.
Find the volume of a sphere whose radius is 2 cm.
Find the volume of a sphere whose diameter is 2.1 m .
A hemispherical bowl is made of steel 0.25 cm thick. The inside radius of the bowl is 5 cm. Find the volume of steel used in making the bowl.
The radius of the internal and external surfaces of a hollow spherical shell are 3 cm and 5 cm respectively. If it is melted and recast into a solid cylinder of heigh2`2/3`cm Find the diameter of the cylinder.
The volume (in cm3) of the greatest sphere that can be cut off from a cylindrical log of wood of base radius 1 cm and height 5 cm is
