Advertisements
Advertisements
प्रश्न
A hose-pipe of cross section area 3 cm2 delivers 1800 liters of water in 10 minutes. Find the speed of water in km/h through the pipe.
उत्तर
Water delivered in 10mins
= 1800liters
= 1800 x 1000cm3
Volume of water
= Speed of water (in cm/m in) x Area of cross-section x Time
1800000 = Speed x 3 x 10
∴ Speed = 60000 cm/mn
`1"cm"/"mn"`
= `(1 + 100000 "km")/(1 + 60"hr")`
= `(60)/(100000)`
= `(6)/(10000)`km/hr
∴ Speed
= `60000 xx (6)/(10000)`km/hr
= 36km/hr
∴ The speed of the water through the pipe is 36km/hr.
APPEARS IN
संबंधित प्रश्न
The following figure shows a solid of uniform cross-section. Find the volume of the solid. All measurements are in centimeters.
Assume that all angles in the figures are right angles.
The following figure shows a solid of uniform cross-section. Find the volume of the solid. All measurements are in centimeters.
Assume that all angles in the figures are right angles.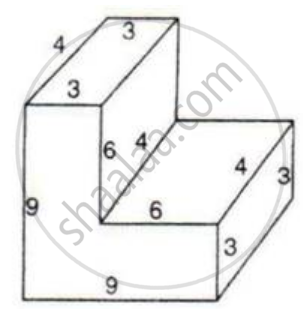
A swimming pool is 40 m long and 15 m wide. Its shallow and deep ends are 1.5 m and 3 m deep respectively. If the bottom of the pool slopes uniformly, find the amount of water in liters required to fill the pool.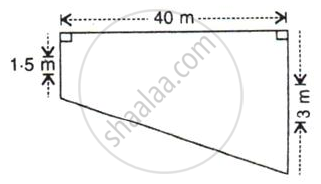
A rectangular water-tank measuring 80 cm x 60 cm is filled form a pipe of cross-sectional area 1.5 cm2, the water emerging at 3.2 m/s. How long does it take to fill the tank?
The internal dimensions of a rectangular box are 12 cm x `x` cm x 9 cm. If the length of the longest rod that can be placed in this box is 17 cm; find `x`.
Find the length of 22 kg copper wire of diameter 0.8 cm, if the weight of 1 cm3 copper is 4.2 g.
Find the length of a solid cylinder of diameter 4 cm when recast into a hollow cylinder of outer diameter 10 cm, thickness 0.25 cm and length 21 cm? Give your answer correct to two decimal places.
The cross section of a piece of metal 2 m in length is shown. Calculate the area of cross section.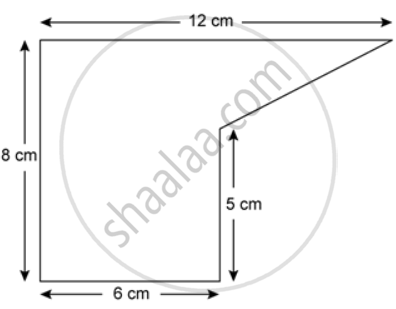
The cross section of a swimming pool is a trapezium whose shallow and deep ends are 1 m and 3 m respectively. If the length of the pool is 50 m and its width is 1.5 m, calculate the volume of water it holds.
The cross section of a canal is a trapezium with the base length of 3 m and the top length of 5 m. It is 2 m deep and 400 m long. Calculate the volume of water it holds.
