Advertisements
Advertisements
प्रश्न
A hose-pipe of cross section area 3 cm2 delivers 1800 liters of water in 10 minutes. Find the speed of water in km/h through the pipe.
उत्तर
Water delivered in 10mins
= 1800liters
= 1800 x 1000cm3
Volume of water
= Speed of water (in cm/m in) x Area of cross-section x Time
1800000 = Speed x 3 x 10
∴ Speed = 60000 cm/mn
`1"cm"/"mn"`
= `(1 + 100000 "km")/(1 + 60"hr")`
= `(60)/(100000)`
= `(6)/(10000)`km/hr
∴ Speed
= `60000 xx (6)/(10000)`km/hr
= 36km/hr
∴ The speed of the water through the pipe is 36km/hr.
APPEARS IN
संबंधित प्रश्न
The following figure shows a closed victory-stand whose dimensions are given in cm.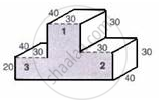
Find the volume and the surface area of the victory stand.
The cross-section of a piece of metal 4 m in length is shown below. Calculate :
(i) The area of the cross-section;
(ii) The volume of the piece of metal in cubic centimeters.
If 1 cubic centimeter of the metal weighs 6.6 g, calculate the weight of the piece of metal to the nearest kg.
A school auditorium is 40 m long, 30 m broad and 12 m high. If each student requires 1.2 m2 of the floor area; find the maximum number of students that can be accommodated in this auditorium. Also, find the volume of air available in the auditorium, for each student.
The cross section of a piece of metal 2 m in length is shown. Calculate the area of cross section.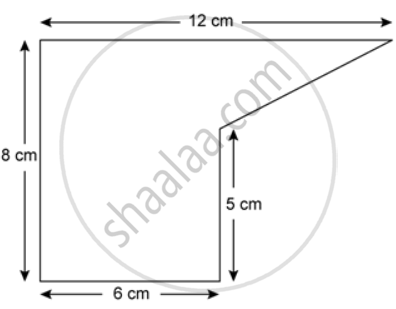
The cross section of a piece of metal 2 m in length
is shown. Calculate the volume of the piece of metal.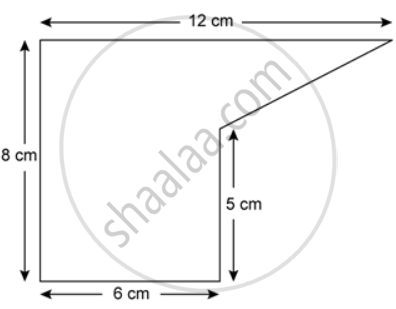
The given figure is a cross -section of a victory stand used in sports. All measurements are in centimetres. Assume all angles in the figure are right angles. If the width of the stand is 60 cm, find The space it occupies in cm3.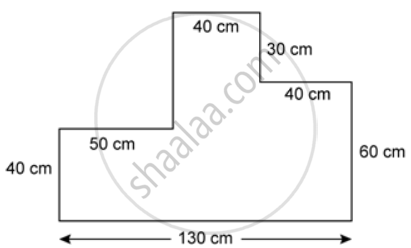
A swimming pool is 50 m long and 15 m wide. Its shallow and deep ends are 1.5 m and 4.5 m respectively. If the bottom of the pool slopes uniformly, find the amount of water in kilolitres required to fill the pool (1 m3 = 1000 liters).
The figure shows the cross section of 0.2 m a concrete wall to be constructed. It is 0.2 m wide at the top, 2.0 m wide at the bottom and its height is 4.0 m, and its length is 40 m. If the whole wall is to be painted, find the cost of painting it at 2.50 per sq m.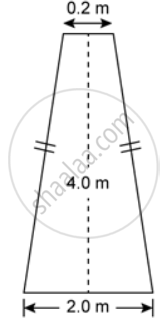
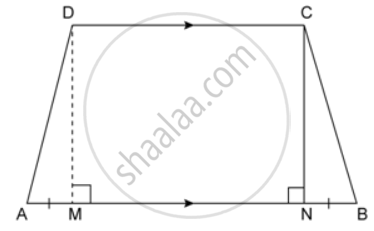
The cross section of a tunnel perpendicular to its length is a trapezium ABCD as shown in the figure. AM = BN; AB = 4.4 m, CD = 3 m The height of a tunnel is 2.4 m. The tunnel is 5.4 m long. Calculate the cost of flooring at the rate of Rs.2. 5 per m2.
ABCDE is the end view of a factory shed which is 50 m long. The roofing of the shed consists of asbestos sheets as shown in the figure. The two ends of the shed are completely closed by brick walls.
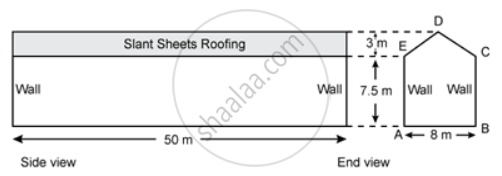
If the cost of asbestos sheet roofing is Rs. 20 per m2, find the cost of roofing.
