Advertisements
Advertisements
प्रश्न
Find the length of 22 kg copper wire of diameter 0.8 cm, if the weight of 1 cm3 copper is 4.2 g.
उत्तर
Diameter of the wire = 0.8cm
Radius of the wire = 0.4cm
If 4.2g of copper = 1cm3 of copper
Then 22kg copper = `(220000)/(4.2)"cm"^3`
Volume of the copper wire = Area of base x length of wire
`(22000)/(4.2)` = πr2 x h
`(22000)/(4.2) = (22)/(7) xx 0.4^2 xx "h"`
h = `(22000 xx 7)/(4.2 xx 22 xx 0.4 xx 0.4)`
h = 10416.7cm
∴ h = 104.17m
∴ The length of the copper wire is 104.17m.
APPEARS IN
संबंधित प्रश्न
A swimming pool is 18 m long and 8 m wide. Its deep and shallow ends are 2 m and 1.2 m respectively. Find the capacity of the pool, assuming that the bottom of the pool slopes uniformly.
A rectangular cardboard sheet has length 32 cm and breadth 26 cm. Squares each of side 3 cm, are cut from the corners of the sheet and the sides are folded to make a rectangular container. Find the capacity of the container formed.
A rectangular water-tank measuring 80 cm x 60 cm is filled form a pipe of cross-sectional area 1.5 cm2, the water emerging at 3.2 m/s. How long does it take to fill the tank?
The cross-section of a piece of metal 4 m in length is shown below. Calculate :
(i) The area of the cross-section;
(ii) The volume of the piece of metal in cubic centimeters.
If 1 cubic centimeter of the metal weighs 6.6 g, calculate the weight of the piece of metal to the nearest kg.
The cross-section of a tunnel perpendicular to its length is a trapezium ABCD as shown in the following figure; also given that:
AM = BN; AB = 7 m; CD = 5 m. The height of the tunnel is 2.4 m. The tunnel is 40 m long. Calculate:
(i) The cost of painting the internal surface of the tunnel (excluding the floor) at the rate of Rs. 5 per m2 (sq. meter).
(ii) The cost of paving the floor at the rate of Rs. 18 per m2.
Find the length of a solid cylinder of diameter 4 cm when recast into a hollow cylinder of outer diameter 10 cm, thickness 0.25 cm and length 21 cm? Give your answer correct to two decimal places.
The cross section of a piece of metal 2 m in length is shown. Calculate the area of cross section.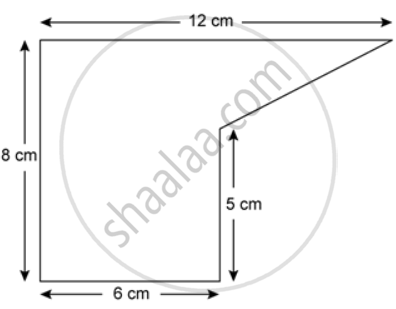
A swimming pool is 50 m long and 15 m wide. Its shallow and deep ends are 1.5 m and 4.5 m respectively. If the bottom of the pool slopes uniformly, find the amount of water in kilolitres required to fill the pool (1 m3 = 1000 liters).
The cross section of a tunnel perpendicular to its length is a trapezium ABCD as shown in the figure. AM = BN; AB = 4.4 m, CD = 3 m The height of a tunnel is 2.4 m. The tunnel is 5.4 m long. Calculate the cost of painting the internal surface of the tunnel (excluding the floor) at the rate of Rs. 5 per m2.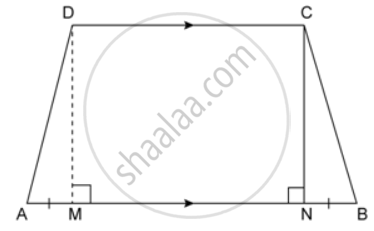
A hose-pipe of cross section area 3 cm2 delivers 1800 liters of water in 10 minutes. Find the speed of water in km/h through the pipe.
