Advertisements
Advertisements
प्रश्न
The cross section of a tunnel perpendicular to its length is a trapezium ABCD as shown in the figure. AM = BN; AB = 4.4 m, CD = 3 m The height of a tunnel is 2.4 m. The tunnel is 5.4 m long. Calculate the cost of painting the internal surface of the tunnel (excluding the floor) at the rate of Rs. 5 per m2.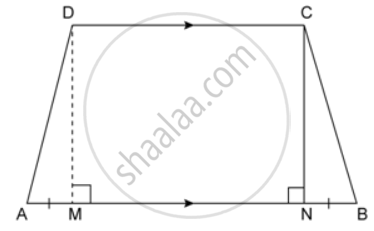
उत्तर
The internal surface area will consist of faces formed by 1 side as length and other sides as AD, CD and BC.
AM = `(1)/(2)("AB" - "CD")`
= `(1)/(2)(4.4 -3)`
AM = 0.7
In ΔAMD, by Pythagoras theorem,
AD2 = AM2 + DM2
AD2 = (0.7)2 + (2.4)2
AD = 2.5m
AD = BC = 2.5n
Total surface area
= (length x AD) + (length x CD) + (length x BC)
= 5.4(AD + CD + BC)
= 5.4(2.5 + 3 + 2.5)
= 43.2m2
Cost of painting
= 43.2 x 5
= Rs,216
∴ The cost of painting the internal surface is Rs.216.
APPEARS IN
संबंधित प्रश्न
A rectangular cardboard sheet has length 32 cm and breadth 26 cm. Squares each of side 3 cm, are cut from the corners of the sheet and the sides are folded to make a rectangular container. Find the capacity of the container formed.
A rectangular water-tank measuring 80 cm x 60 cm is filled form a pipe of cross-sectional area 1.5 cm2, the water emerging at 3.2 m/s. How long does it take to fill the tank?
Find the length of 22 kg copper wire of diameter 0.8 cm, if the weight of 1 cm3 copper is 4.2 g.
The cross section of a piece of metal 2 m in length is shown. Calculate the area of cross section.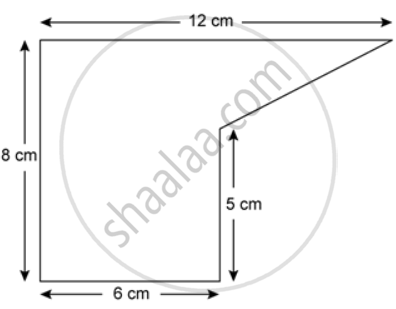
The cross section of a piece of metal 2 m in length
is shown. Calculate the volume of the piece of metal.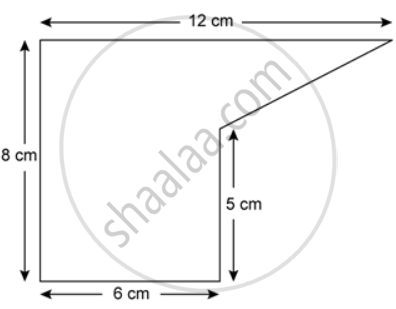
A swimming pool is 50 m long and 15 m wide. Its shallow and deep ends are 1.5 m and 4.5 m respectively. If the bottom of the pool slopes uniformly, find the amount of water in kilolitres required to fill the pool (1 m3 = 1000 liters).
ABCDE is the end view of a factory shed which is 50 m long. The roofing of the shed consists of asbestos sheets as shown in the figure. The two ends of the shed are completely closed by brick walls.
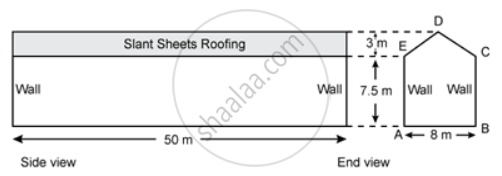
If the cost of asbestos sheet roofing is Rs. 20 per m2, find the cost of roofing.
ABCDE is the end view of a factory shed which is 50 m long. The roofing of the shed consists of asbestos sheets as shown in the figure. The two ends of the shed are completely closed by brick walls.
Find the total surface area (including roofing) of the shed.
The cross section of a swimming pool is a trapezium whose shallow and deep ends are 1 m and 3 m respectively. If the length of the pool is 50 m and its width is 1.5 m, calculate the volume of water it holds.
A hose-pipe of cross section area 3 cm2 delivers 1800 liters of water in 10 minutes. Find the speed of water in km/h through the pipe.
