Advertisements
Advertisements
प्रश्न
ABCDE is the end view of a factory shed which is 50 m long. The roofing of the shed consists of asbestos sheets as shown in the figure. The two ends of the shed are completely closed by brick walls.
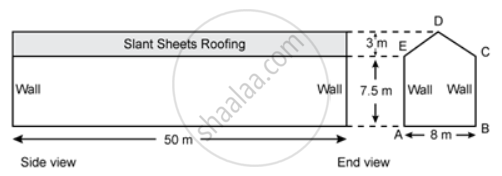
If the cost of asbestos sheet roofing is Rs. 20 per m2, find the cost of roofing.
उत्तर
Asbestos sheets are spread on the area formed by the rectangle with CD and DE as lengths.
In ΔCDE, by Pythagoras theorem,
DE2 = `("perpendicular")^2 + ("Ab"/2)^2`
DE2 = `3^2 + (8/2)^2`
DE2 = 32 + 42
DE2 = 25
∴ DE = CD = 5m
Area of asbestos sheets = DE x length + Dc x length
Area of asbestos sheet
= 2 x 5 x 50
= 500m2
Cost of roofing
= Area x rate
= 500 x 20
= Rs.10,000
∴ The cost of roofing is Rs.10,000.
APPEARS IN
संबंधित प्रश्न
The following figure shows a solid of uniform cross-section. Find the volume of the solid. All measurements are in centimeters.
Assume that all angles in the figures are right angles.
The following figure shows a closed victory-stand whose dimensions are given in cm.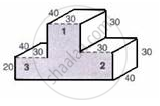
Find the volume and the surface area of the victory stand.
A swimming pool is 18 m long and 8 m wide. Its deep and shallow ends are 2 m and 1.2 m respectively. Find the capacity of the pool, assuming that the bottom of the pool slopes uniformly.
The figure represents the cross section of a swimming pool 10 m broad, 2 m deep at one end, 3 m deep at the other end. Calculate the volume of water it will hold when full, given that its length is 40 m.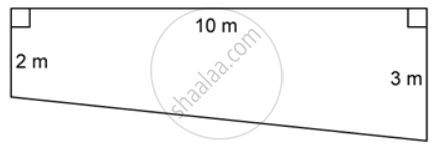
The given figure is a cross -section of a victory stand used in sports. All measurements are in centimetres. Assume all angles in the figure are right angles. If the width of the stand is 60 cm, find The total surface area in m2.
The figure shows the cross section of 0.2 m a concrete wall to be constructed. It is 0.2 m wide at the top, 2.0 m wide at the bottom and its height is 4.0 m, and its length is 40 m. Calculate the cross sectional area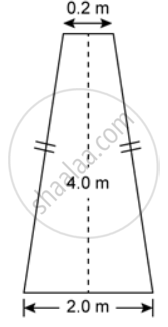
The figure shows the cross section of 0.2 m a concrete wall to be constructed. It is 0.2 m wide at the top, 2.0 m wide at the bottom and its height is 4.0 m, and its length is 40 m. Calculate the volume of the concrete in the wall

The cross section of a tunnel perpendicular to its length is a trapezium ABCD as shown in the figure. AM = BN; AB = 4.4 m, CD = 3 m The height of a tunnel is 2.4 m. The tunnel is 5.4 m long. Calculate the cost of painting the internal surface of the tunnel (excluding the floor) at the rate of Rs. 5 per m2.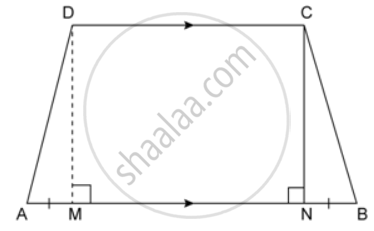
The cross section of a tunnel perpendicular to its length is a trapezium ABCD as shown in the figure. AM = BN; AB = 4.4 m, CD = 3 m The height of a tunnel is 2.4 m. The tunnel is 5.4 m long. Calculate the cost of flooring at the rate of Rs.2. 5 per m2.

The cross section of a swimming pool is a trapezium whose shallow and deep ends are 1 m and 3 m respectively. If the length of the pool is 50 m and its width is 1.5 m, calculate the volume of water it holds.
