Advertisements
Advertisements
प्रश्न
A lens forms a real image 3 cm high of an object 1 cm high. If the separation of object and image is 15 cm, find the focal length of the lens.
उत्तर
Given,
Height of image (h') = - 3 cm (negative because image is real)
Height of object = 1 cm
Let us first define the sign convention:
Since the object distance is always negative, let it be -u.
Since the focal length is positive for a convex lens, let it be +f .
Magnification =`h/h=v/u`
`v/u=-3`
(i) Since object distance (u) is always negative, and the ratio `v/u` here is negative, v must be positive, i.e., it is on the right side of the lens.
Now, we have object distance + image distance = 15
`v+(-u)=15 (using sign convention)`
`-3u-u=15`
`-4u=15`
`u=(-15)/4`
Applying the lens formula:
`1/f=1/v-1/u`
`1/f=1/(-3u)-1/u`
`1/f=(-4)/(3u)`
`f=(3u)/-4=(3xx-15/4)/4=45/16=2.81`cm
Hence, the focal length of the lens is +2.81 cm.
APPEARS IN
संबंधित प्रश्न
Explain the following term related to spherical lenses:- centres of curvature
The shiny outer surface of a hollow sphere of aluminium of radius 50 cm is to be used as a mirror:
State whether this spherical mirror will diverge or converge light rays.
A diverging lens is used in:
(a) a magnifying glass
(b) a car to see objects on rear side
(c) spectacles for the correction of short sight
(d) a simple camera
Name the mirrors shown in Figure (a) and (b).
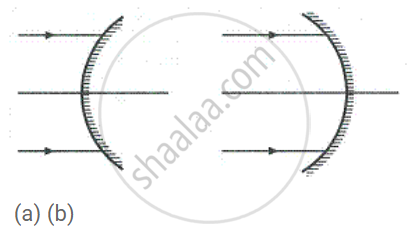
Upto what maximum distance from a concave mirror, the image can be obtained? What will be the location of object for it?
An object forms a virtual image which is 1/8th of the size of the object. If the object is placed at a distance of 40 cm from the convex mirror, calculate:
- the position of the image
- the focal length of the convex mirror.
What is the relation between focal length and radius of curvature of a concave mirror?
Define the term Centre of curvature.
The spherical mirror used in a beauty parlour as make-up mirror is _______.
