Advertisements
Advertisements
Question
A lens forms a real image 3 cm high of an object 1 cm high. If the separation of object and image is 15 cm, find the focal length of the lens.
Solution
Given,
Height of image (h') = - 3 cm (negative because image is real)
Height of object = 1 cm
Let us first define the sign convention:
Since the object distance is always negative, let it be -u.
Since the focal length is positive for a convex lens, let it be +f .
Magnification =`h/h=v/u`
`v/u=-3`
(i) Since object distance (u) is always negative, and the ratio `v/u` here is negative, v must be positive, i.e., it is on the right side of the lens.
Now, we have object distance + image distance = 15
`v+(-u)=15 (using sign convention)`
`-3u-u=15`
`-4u=15`
`u=(-15)/4`
Applying the lens formula:
`1/f=1/v-1/u`
`1/f=1/(-3u)-1/u`
`1/f=(-4)/(3u)`
`f=(3u)/-4=(3xx-15/4)/4=45/16=2.81`cm
Hence, the focal length of the lens is +2.81 cm.
APPEARS IN
RELATED QUESTIONS
Define the following term in the context of spherical mirrors:- Principal focus
What type of image is formed:
on a cinema screen?
The shiny outer surface of a hollow sphere of aluminium of radius 50 cm is to be used as a mirror:
State whether this spherical mirror will diverge or converge light rays.
If a spherical mirror breaks, what type of mirrors are the individual pieces?
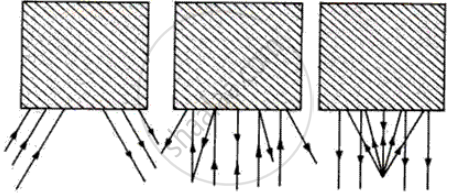
The boxes in figure (a, b, c) represent mirrors; insert a mirror which will reflect the incident ray as shown in the diagram.
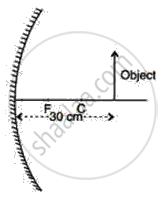
An object is placed in front of a concave mirror as shown in the following figure. By scale drawing, find the nature of the image. Given f = 10 cm, v = 30 cm.
Define focal length.
