Advertisements
Advertisements
प्रश्न
A manufacturer considers that men and women workers are equally efficient and so he pays them at the same rate. He has 30 and 17 units of workers (male and female) and capital respectively, which he uses to produce two types of goods A and B. To produce one unit of A, 2 workers and 3 units of capital are required while 3 workers and 1 unit of capital is required to produce one unit of B. If A and B are priced at ₹100 and ₹120 per unit respectively, how should he use his resources to maximise the total revenue? Form the above as an LPP and solve graphically. Do you agree with this view of the manufacturer that men and women workers are equally efficient and so should be paid at the same rate?
उत्तर
Let x units of A and y units of B be produced by the manufacturer.
The price of one unit of A is ₹100 and the price of one unit of B is ₹120. Therefore, the total price of x units of A and y units of B or the total revenue is ₹(100x + 120y).
One unit of A requires 2 workers and one unit of B requires 3 workers. Therefore, xunits of A and y units of B requires (2x + 3y) workers. But, the manufacturer has 30 workers.
∴ 2x + 3y ≤ 30
Similarly, one unit of A requires 3 units of capital and one unit of B requires 1 unit of capital. Therefore, x units of A and y units of B requires (3x + y) units of capital. But, the manufacturer has 17 units of capital.
∴ 3x + y ≤ 17
Thus, the given linear programming problem is
Maximise Z = 100x + 120y
subject to the constraints
2x + 3y ≤ 30
3x + y ≤ 17
x, y ≥ 0
The feasible region determined by the given constraints can be diagrammatically represented as,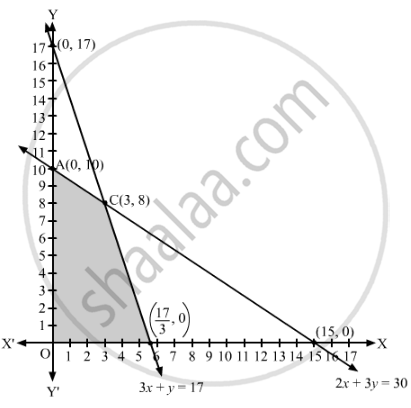
The coordinates of the corner points of the feasible region are O(0, 0), A(0, 10), B \[\left( \frac{17}{3}, 0 \right)\] and C(3, 8).
The value of the objective function at these points are given in the following table.
| Corner Point | Z = 100x + 120y |
| (0, 0) | 100 × 0 + 120 × 0 = 0 |
| (0, 10) | 100 × 0 + 120 × 10 = 1200 |
|
\[\left( \frac{17}{3}, 0 \right)\]
|
100 ×\[\frac{17}{3}\] + 120 × 0 = \[\frac{1700}{3}\] |
| (3, 8) | 100 × 3 + 120 × 8 = 1260 → Maximum |
Hence, the maximum total revenue is ₹1,260 when 3 units of A and 8 units of B are produced.
Yes, because the efficiency of a worker does not depend on whether the worker is a male or a female.
APPEARS IN
संबंधित प्रश्न
Minimize `z=4x+5y ` subject to `2x+y>=7, 2x+3y<=15, x<=3,x>=0, y>=0` solve using graphical method.
Solve the following LPP by graphical method:
Maximize: z = 3x + 5y
Subject to: x + 4y ≤ 24
3x + y ≤ 21
x + y ≤ 9
x ≥ 0, y ≥ 0
Maximise Z = x + 2y subject to the constraints
`x + 2y >= 100`
`2x - y <= 0`
`2x + y <= 200`
Solve the above LPP graphically
Solve the following linear programming problem graphically :
Maximise Z = 7x + 10y subject to the constraints
4x + 6y ≤ 240
6x + 3y ≤ 240
x ≥ 10
x ≥ 0, y ≥ 0
Solve the following L.P.P. graphically:
Minimise Z = 5x + 10y
Subject to x + 2y ≤ 120
Constraints x + y ≥ 60
x – 2y ≥ 0 and x, y ≥ 0
Minimize Z = 18x + 10y
Subject to
\[4x + y \geq 20\]
\[2x + 3y \geq 30\]
\[ x, y \geq 0\]
Maximize Z = 4x + 3y
subject to
\[3x + 4y \leq 24\]
\[8x + 6y \leq 48\]
\[ x \leq 5\]
\[ y \leq 6\]
\[ x, y \geq 0\]
Solve the following linear programming problem graphically:
Minimize z = 6 x + 3 y
Subject to the constraints:
4 x + \[y \geq\] 80
x + 5 \[y \geq\] 115
3 x + 2 \[y \leq\] 150
\[x \geq\] 0 , \[y \geq\] 0
A hospital dietician wishes to find the cheapest combination of two foods, A and B, that contains at least 0.5 milligram of thiamin and at least 600 calories. Each unit of Acontains 0.12 milligram of thiamin and 100 calories, while each unit of B contains 0.10 milligram of thiamin and 150 calories. If each food costs 10 paise per unit, how many units of each should be combined at a minimum cost?
Kellogg is a new cereal formed of a mixture of bran and rice that contains at least 88 grams of protein and at least 36 milligrams of iron. Knowing that bran contains 80 grams of protein and 40 milligrams of iron per kilogram, and that rice contains 100 grams of protein and 30 milligrams of iron per kilogram, find the minimum cost of producing this new cereal if bran costs Rs 5 per kg and rice costs Rs 4 per kg
A wholesale dealer deals in two kinds, A and B (say) of mixture of nuts. Each kg of mixture A contains 60 grams of almonds, 30 grams of cashew nuts and 30 grams of hazel nuts. Each kg of mixture B contains 30 grams of almonds, 60 grams of cashew nuts and 180 grams of hazel nuts. The remainder of both mixtures is per nuts. The dealer is contemplating to use mixtures A and B to make a bag which will contain at least 240 grams of almonds, 300 grams of cashew nuts and 540 grams of hazel nuts. Mixture A costs Rs 8 per kg. and mixture B costs Rs 12 per kg. Assuming that mixtures A and B are uniform, use graphical method to determine the number of kg. of each mixture which he should use to minimise the cost of the bag.
A manufacturer has three machines installed in his factory. machines I and II are capable of being operated for at most 12 hours whereas Machine III must operate at least for 5 hours a day. He produces only two items, each requiring the use of three machines. The number of hours required for producing one unit each of the items on the three machines is given in the following table:
| Item | Number of hours required by the machine | ||
A B |
I | II | III |
| 1 2 |
2 1 |
1 5/4 |
|
He makes a profit of Rs 6.00 on item A and Rs 4.00 on item B. Assuming that he can sell all that he produces, how many of each item should he produces so as to maximize his profit? Determine his maximum profit. Formulate this LPP mathematically and then solve it.
A manufacturer produces two types of steel trunks. He has two machines A and B. For completing, the first types of the trunk requires 3 hours on machine A and 3 hours on machine B, whereas the second type of the trunk requires 3 hours on machine A and 2 hours on machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs 30 and Rs 25 per trunk of the first type and the second type respectively. How many trunks of each type must he make each day to make maximum profit?
An aeroplane can carry a maximum of 200 passengers. A profit of Rs 400 is made on each first class ticket and a profit of Rs 600 is made on each economy class ticket. The airline reserves at least 20 seats of first class. However, at least 4 times as many passengers prefer to travel by economy class to the first class. Determine how many each type of tickets must be sold in order to maximize the profit for the airline. What is the maximum profit.
A firm makes items A and B and the total number of items it can make in a day is 24. It takes one hour to make an item of A and half an hour to make an item of B. The maximum time available per day is 16 hours. The profit on an item of A is Rs 300 and on one item of B is Rs 160. How many items of each type should be produced to maximize the profit? Solve the problem graphically.
A box manufacturer makes large and small boxes from a large piece of cardboard. The large boxes require 4 sq. metre per box while the small boxes require 3 sq. metre per box. The manufacturer is required to make at least three large boxes and at least twice as many small boxes as large boxes. If 60 sq. metre of cardboard is in stock, and if the profits on the large and small boxes are Rs 3 and Rs 2 per box, how many of each should be made in order to maximize the total profit?
An oil company has two depots, A and B, with capacities of 7000 litres and 4000 litres respectively. The company is to supply oil to three petrol pumps, D, E, F whose requirements are 4500, 3000 and 3500 litres respectively. The distance (in km) between the depots and petrol pumps is given in the following table:
Figure
Assuming that the transportation cost per km is Rs 1.00 per litre, how should the delivery be scheduled in order that the transportation cost is minimum?
The region represented by the inequation system x, y ≥ 0, y ≤ 6, x + y ≤ 3 is
A farmer has a supply of chemical fertilizer of type A which contains 10% nitrogen and 6% phosphoric acid and of type B which contains 5% nitrogen and 10% phosphoric acid. After the soil test, it is found that at least 7 kg of nitrogen and the same quantity of phosphoric acid is required for a good crop. The fertilizer of type A costs ₹ 5.00 per kg and the type B costs ₹ 8.00 per kg. Using Linear programming, find how many kilograms of each type of fertilizer should be bought to meet the requirement and for the cost to be minimum. Find the feasible region in the graph.
A manufacturer has employed 5 skilled men and 10 semi-skilled men and makes two models A and B of an article. The making of one item of model A requires 2 hours of work by a skilled man and 2 hours work by a semi-skilled man. One item of model B requires 1 hour by a skilled man and 3 hours by a semi-skilled man. No man is expected to work more than 8 hours per day. The manufacturer's profit on an item of model A is ₹ 15 and on an item of model B is ₹ 10. How many items of each model should be made per day in order to maximize daily profit? Formulate the above LPP and solve it graphically and find the maximum profit.
Maximum value of 4x + 13y subject to constraints x ≥ 0, y ≥ 0, x + y ≤ 5 and 3x + y ≤ 9 is ______.
The maximum value of z = 6x + 8y subject to x - y ≥ 0, x + 3y ≤ 12, x ≥ 0, y ≥ 0 is ______.
The maximum value of Z = 5x + 4y, Subject to y ≤ 2x, x ≤ 2y, x + y ≤ 3, x ≥ 0, y ≥ 0 is ______.
For the function z = 19x + 9y to be maximum under the constraints 2x + 3y ≤ 134, x + 5y ≤ 200, x ≥ 0, y ≥ 0; the values of x and y are ______.
For the LPP, maximize z = x + 4y subject to the constraints x + 2y ≤ 2, x + 2y ≥ 8, x, y ≥ 0 ______.
In the Corner point method for solving a linear programming problem the second step after finding the feasible region of the linear programming problem and determining its corner points is ____________.
The corner points of the bounded feasible region of a LPP are A(0,50), B(20, 40), C(50, 100) and D(0, 200) and the objective function is Z = x + 2y. Then the maximum value is ____________.
The comer point of the feasible region determined by the following system of linear inequalities:
2x + y ≤ 10, x + 3y ≤ 15, x, y ≥ 0 are (0, 0), (5, 0), (3, 4) and (0, 5). Let x = Px + qx where P, q > 0 condition on P and Q so that the maximum of z occurs at both (3, 4) and (0, 5) is
The maximum value of z = 5x + 2y, subject to the constraints x + y ≤ 7, x + 2y ≤ 10, x, y ≥ 0 is ______.
The maximum value of 2x + y subject to 3x + 5y ≤ 26 and 5x + 3y ≤ 30, x ≥ 0, y ≥ 0 is ______.
Solve the following linear programming problem graphically:
Minimize: Z = 5x + 10y
Subject to constraints:
x + 2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0, x ≥ 0, y ≥ 0.
Solve the following Linear Programming problem graphically:
Maximize: Z = 3x + 3.5y
Subject to constraints:
x + 2y ≥ 240,
3x + 1.5y ≥ 270,
1.5x + 2y ≤ 310,
x ≥ 0, y ≥ 0.
The feasible region corresponding to the linear constraints of a Linear Programming Problem is given below.
Which of the following is not a constraint to the given Linear Programming Problem?
Find feasible solution for the following system of linear inequation graphically.
3x + 4y ≥ 12, 4x + 7y ≤ 28, x ≥ 0, y ≥ 0
A linear programming problem is given by Z = px + qy where p, q > 0 subject to the constraints: x + y ≤ 60, 5x + y ≤ 100, x ≥ 0 and y ≥ 0
- Solve graphically to find the corner points of the feasible region.
- If Z = px + qy is maximum at (0, 60) and (10, 50), find the relation of p and q. Also mention the number of optimal solution(s) in this case.
