Advertisements
Advertisements
प्रश्न
A motorbike, initially at rest, picks up a velocity of 72 kmh−1 over a distance of 40 m. Calculate
- acceleration
- time in which it picks up above velocity.
उत्तर
Initial velocity = u = 0
Final velocity = v = 72 km/h = `72xx5/18` m/s
v = 20 m/s
Distance = S = 40 m
(i) v2 − u2 = 2aS
(20)2 − (0)2 = 2a (40)
80a = 400
a = `400/80`
a = 5 ms−2
(ii) v = u + at
20 = 0 + 5t
5t = 20
t = `20/5`
t = 4 s
APPEARS IN
संबंधित प्रश्न
An object of mass 16 kg is moving with an acceleration of 3 m/s2. Calculate the applied force. If the same force is applied to an object of mass 24 kg, how much will be the acceleration?
A toy car initially moving with uniform velocity of 18 km h-1 comes to a stop in 2 s. Find the retardation of the car in S.I. units.
The change in velocity of a motorbike is 54 kmh−1 in one minute. Calculate its acceleration in (a) ms−2 (b) kmh−2.
A motor bike running at 90 kmh−1 is slowed down to 18 kmh−1 in 2.5 s. Calculate
- acceleration
- distance covered during slow down.
The graph shows how the velocity of a scooter varies with time in 50 s.
Work out: Deceleration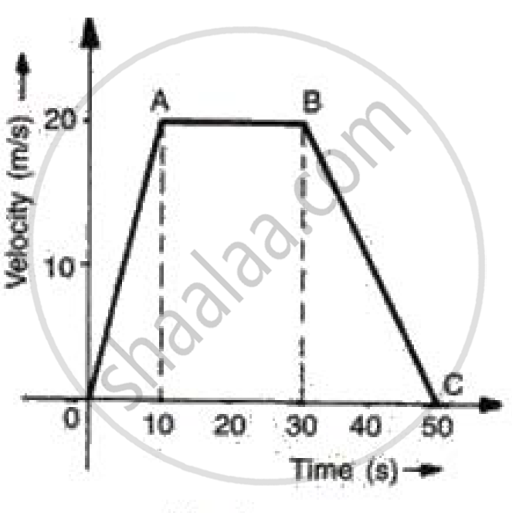
A car accelerates to a velocity of 30 m/s in 10 s and then decelerates for 20 s so that it stops. Draw a velocity-time graph to represent the motion and find:
The acceleration.
Correct your friend who says that acceleration gives the idea of how fast the position changes.
Acceleration is a scalar.
An object can be moving with uniform speed but with variable acceleration.
