Advertisements
Advertisements
प्रश्न
A motorcycle moving with a speed of 5 m/s is subjected to an acceleration of 0.2 m/s2. Calculate the speed of the motorcycle after 10 seconds, and the distance travelled in this time.
उत्तर
We have to find the distance travelled and final velocity of the body. We have the following information given,
Initial velocity, (u) = 5 m/s
Acceleration, (a) = 0.2 m/s2
Time taken, (t) = 10 s
So, we can find the final velocity using the relation,
v = u + at
So, final velocity,
v = 5 + (0.2)(10)
= 7 m/s
We can calculate the distance travelled by using the 2nd equation of motion,
`s = ut + 1/2 at^2`
Put the values in above equation to find the distance travelled by the motorcycle ,
`(s) = 5(10) + 1/2(0.2)(10)^2`
= (50 + 10) m
= 60 m
APPEARS IN
संबंधित प्रश्न
When will you say a body is at non-uniform acceleration?
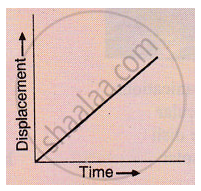
What conclusion can you draw about the velocity of a body from the displacement-time graph shown below :
Derive the formula s= `ut+1/2at^2` , where the symbols have usual meanings.
A train starting from stationary position and moving with uniform acceleration attains a speed of 36 km per hour in 10 minutes. Find its acceleration.
A freely falling object travels 4.9 m in 1st second, 14.7 m in 2 nd second, 24.5 m in 3rd second, and so on. This data shows that the motion of a freely falling object is a case of :
If a stone and a pencil are dropped simultaneously in vacuum from the top of a tower, then which of the two will reach the ground first? Give reason.
The figure shows the displacement - time graph for four bodies A, B C and D. In each case state what information do you get about the acceleration (zero, positive or negative).

Can you suggest a real-life example about the motion of a body from the following velocity – time graph?
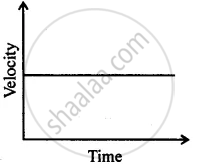
Can you suggest a real-life example about the motion of a body from the following velocity – time graph?
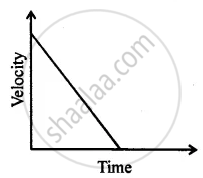
The velocity-time graph (Fig. 8.5) shows the motion of a cyclist. Find (i) its acceleration (ii) its velocity and (iii) the distance covered by the cyclist in 15 seconds.

