Advertisements
Advertisements
Question
A motorcycle moving with a speed of 5 m/s is subjected to an acceleration of 0.2 m/s2. Calculate the speed of the motorcycle after 10 seconds, and the distance travelled in this time.
Solution
We have to find the distance travelled and final velocity of the body. We have the following information given,
Initial velocity, (u) = 5 m/s
Acceleration, (a) = 0.2 m/s2
Time taken, (t) = 10 s
So, we can find the final velocity using the relation,
v = u + at
So, final velocity,
v = 5 + (0.2)(10)
= 7 m/s
We can calculate the distance travelled by using the 2nd equation of motion,
`s = ut + 1/2 at^2`
Put the values in above equation to find the distance travelled by the motorcycle ,
`(s) = 5(10) + 1/2(0.2)(10)^2`
= (50 + 10) m
= 60 m
APPEARS IN
RELATED QUESTIONS
Fill in the following blank with suitable word :
A motorcycle has a steady……………. of 3 m/s2. This means that every………………. its…………….. increases by………….
What is meant by the term acceleration ? State the SI unit of acceleration.
Derive the following equations for uniformly accelerated motion:
(i) v = u + at
(ii) `"S = ut" + 1/2 "at"^2`
(iii) v2 = u2 + 2aS
where the symbols have their usual meanings.
What do you understand by the term acceleration?
Multiple choice Question. Select the correct option.
A body dropped from the top of a tower reaches the ground in 4s. Height of the tower is
How can you find the following?
Acceleration from velocity – time graph.
Can you suggest a real-life example about the motion of a body from the following velocity – time graph?
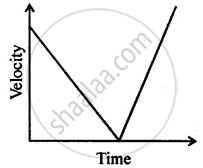
Area under a v – t graph represents a physical quantity which has the unit
The velocity-time graph (Fig. 8.5) shows the motion of a cyclist. Find (i) its acceleration (ii) its velocity and (iii) the distance covered by the cyclist in 15 seconds.

Two stones are thrown vertically upwards simultaneously with their initial velocities u1 and u2 respectively. Prove that the heights reached by them would be in the ratio of `"u"_1^2 : "u"_2^2` (Assume upward acceleration is –g and downward acceleration to be +g)
