Advertisements
Advertisements
प्रश्न
A myopic adult has a far point at 0.1 m. His power of accomodation is 4 diopters.
- What power lenses are required to see distant objects?
- What is his near point without glasses?
- What is his near point with glasses? (Take the image distance from the lens of the eye to the retina to be 2 cm.)
उत्तर
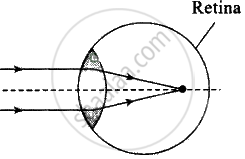 (a) Defected eye |
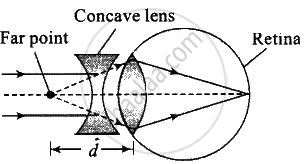 (b) Removal of Defect |
`1/f = 1/f_1 + 1/f_2`
In terms of power P = P1 + P2
i. If for the normal relaxed eye of an average person, the power at the far point be `P_f`. The required power
`P_f = 1/f = 1/0.1 + 1/0.2` = 60 D
By the corrective lens the object distance at the far point is `oo`
The power required is `P_f^' = 1/f^' = 1/(oo) + 1/0.02` = 50 D
Now for eye + lens system, we have the sum of the eye and that of the glasses `P_g`
`P_f^' = P_f + P_g` ⇒ 50 D = 60 D + `P_g`
Which gives, `P_g` = – 10 D
ii. For the normal eye his power of accommodation is 4 D, Let the power of the normal eye for near vision be `P_n`.
Then, 4 = `P_n = P_f` or `P_n` = 64 D
Let his near point be `x_n`, then
`1/x_n + 1/0.02` = 64 to `1/x_n + 50` = 64
`1/x_n` = 14 ⇒ `x_n = 1/14 m` = 0.07 m
iii. With glasses `P_n^' = P_f^' + 4` = 54
54 = `1/x_n^' + 1/0.02 = 1/x_n^' + 50`
`1/x_n` = 14 ⇒ `x_n^' = 1/4 m` = 0.25 m
APPEARS IN
संबंधित प्रश्न
A virtual image, we always say, cannot be caught on a screen. Yet when we ‘see’ a virtual image, we are obviously bringing it on to the ‘screen’ (i.e., the retina) of our eye. Is there a contradiction?
For a normal eye, the far point is at infinity and the near point of distinct vision is about 25cm in front of the eye. The cornea of the eye provides a converging power of about 40 dioptres, and the least converging power of the eye-lens behind the cornea is about 20 dioptres. From this rough data estimate the range of accommodation (i.e., the range of converging power of the eye-lens) of a normal eye.
A myopic person has been using spectacles of power −1.0 dioptre for distant vision. During old age, he also needs to use the separate reading glass of power + 2.0 dioptres. Explain what may have happened.
What should be the distance between the object and the magnifying glass if the virtual image of each square in the figure is to have an area of 6.25 mm2. Would you be able to see the squares distinctly with your eyes very close to the magnifier?
The muscles of a normal eye are least strained when the eye is focussed on an object
A person A can clearly see objects between 25 cm and 200 cm. Which of the following may represent the range of clear vision for a person B having muscles stronger than A, but all other parameters of eye identical to that of A?
The distance of the eye-lens from the retina is x. For a normal eye, the maximum focal length of the eye-lens
A man wearing glasses of focal length +1 m cannot clearly see beyond 1 m
A person looks at different trees in an open space with the following details. Arrange the trees in decreasing order of their apparent sizes.
| Tree | Height(m) | Distance from the eye(m) |
| A | 2.0 | 50 |
| B | 2.5 | 80 |
| C | 1.8 | 70 |
| D | 2.8 | 100 |
A nearsighted person cannot see beyond 25 cm. Assuming that the separation of the glass from the eye is 1 cm, find the power of lens needed to see distant objects.
