Advertisements
Advertisements
प्रश्न
A parallel-plate capacitor of plate area A and plate separation d is charged to a potential difference V and then the battery is disconnected. A slab of dielectric constant K is then inserted between the plates of the capacitor so as to fill the space between the plates. Find the work done on the system in the process of inserting the slab.
उत्तर
Initial capacitance, `C = (∈_0A)/d`
The energy of the capacitor before the insertion of the dielectric is given by `E_1 = 1/2 CV^2 = 1/2 (∈_0A)/d V^2`
After inserting the dielectric slab, the capacitance becomes
`C_1 = KC = K(∈_0A)/d`
and the final voltage becomes
`V_1 = V/K`
Thus, the final energy stored in the capacitor is given by
`E_2 = 1/2 (K∈_0A)/d xx (V/K)^2`
⇒ `E_2 = 1/2 (∈_0AV^2)/(Kd)`
Now ,
Work done = Change in energy
`therefore W = E_2 - E_1`
⇒ `W = 1/2 (∈_0AV^2)/(Kd) - 1/2(∈_0AV^2)/(d)`
⇒ `W = 1/2(∈_0AV^2)/(d)(1/K-1)`
APPEARS IN
संबंधित प्रश्न
As `C = (1/V) Q` , can you say that the capacitance C is proportional to the charge Q?
Two metal spheres of capacitance C1 and C2 carry some charges. They are put in contact and then separated. The final charges Q1 and Q2 on them will satisfy
The plates of a parallel-plate capacitor are made of circular discs of radii 5⋅0 cm each. If the separation between the plates is 1⋅0 mm, what is the capacitance?
The outer cylinders of two cylindrical capacitors of capacitance 2⋅2 µF each, are kept in contact and the inner cylinders are connected through a wire. A battery of emf 10 V is connected as shown in figure . Find the total charge supplied by the battery to the inner cylinders.

Two conducting spheres of radii R1 and R2 are kept widely separated from each other. What are their individual capacitances? If the spheres are connected by a metal wire, what will be the capacitance of the combination? Think in terms of series−parallel connections.
It is required to construct a 10 µF capacitor which can be connected across a 200 V battery. Capacitors of capacitance 10 µF are available but they can withstand only 50 V. Design a combination which can yield the desired result.
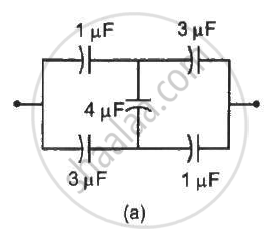
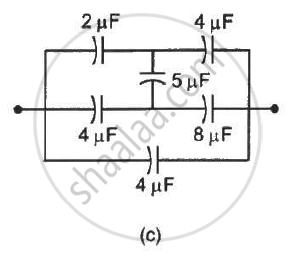
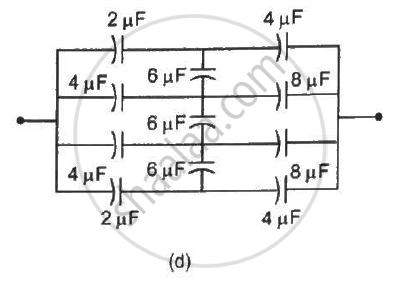
Find the equivalent capacitances of the combinations shown in figure between the indicated points.

Find the capacitance of the combination shown in figure between A and B.

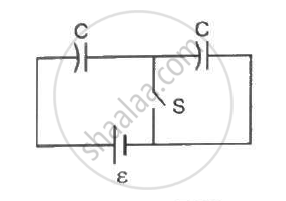
Consider the situation shown in the figure. The switch S is open for a long time and then closed. (a) Find the charge flown through the battery when the switch S is closed. (b) Find the work done by the battery.(c) Find the change in energy stored in the capacitors.(d) Find the heat developed in the system.
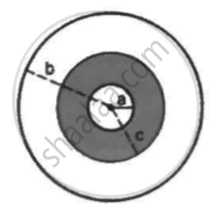
A sphercial capacitor is made of two conducting spherical shells of radii a and b. The space between the shells is filled with a dielectric of dielectric constant K up to a radius c as shown in figure . Calculate the capacitance.
Consider an assembly of three conducting concentric spherical shell of radii a, b and c as shown in figure Find the capacitance of the assembly between the points Aand B.

Obtain the expression for capacitance for a parallel plate capacitor.
Derive the expression for resultant capacitance, when the capacitor is connected in parallel.
Dielectric constant for a metal is ______.
The radius of a sphere of capacity 1 microfarad in the air is ______
A parallel plate capacitor is filled by a dielectric whose relative permittivity varies with the applied voltage (U) as ε = αU where α = 2V–1. A similar capacitor with no dielectric is charged to U0 = 78V. It is then connected to the uncharged capacitor with the dielectric. Find the final voltage on the capacitors.
A 5µF capacitor is charged fully by a 220 V supply. It is then disconnected from the supply and is connected in series to another uncharged 2.5 µF capacitor If the energy change during the charge redistribution is `"X"/100`J then value of X to the 100 nearest integer is ______.
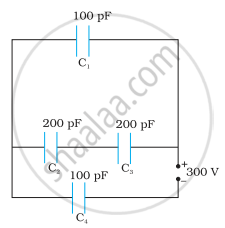
Obtain the equivalent capacitance of the network shown in the figure. For a 300 V supply, determine the charge on each capacitor.