Advertisements
Advertisements
प्रश्न
A particle moves in a closed orbit around the origin, due to a force which is directed towards the origin. The de Broglie wavelength of the particle varies cyclically between two values λ1, λ2 with λ1 > λ2. Which of the following statement are true?
- The particle could be moving in a circular orbit with origin as centre.
- The particle could be moving in an elliptic orbit with origin as its focus.
- When the de Broglie wavelength is λ1, the particle is nearer the origin than when its value is λ2.
- When the de Broglie wavelength is λ2, the particle is nearer the origin than when its value is λ1.
पर्याय
b and d
a and c
b, c and d
a, c and d
उत्तर
b and d
Explanation:
According to the question, here given that the de-Broglie wavelength of the particle can be varying cyclically between two values λ1 and λ2, it is possible if particle is moving in an elliptical orbit with origin as its one focus.
As shown in the figure given alongside,
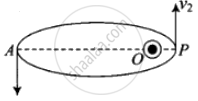
Let v1 and v2 be the speed of particle at A and B respectively and origin is at focus O. If λ1 and λ2 are the de-Broglie wavelengths associated with particle while moving at A and B respectively, then `λ_1 = h/(mv_1)`
And `λ_2 = h/(mv_2)`
∴ `λ_1/λ_2 = v_2/v_1`
Since `λ_1 > λ_2`
∴ `v_2 > v_1`
By the law of conservation of angular momentum, the particle moves faster when it is closer to focus.
From figure, we note that origin O is closed to P than A.
APPEARS IN
संबंधित प्रश्न
Calculate the de Broglie wavelength of the electrons accelerated through a potential difference of 56 V.
For what kinetic energy of a neutron will the associated de Broglie wavelength be 1.40 × 10−10 m?
Find the de Broglie wavelength of a neutron, in thermal equilibrium with matter, having an average kinetic energy of `(3/2)` kT at 300 K.
What is the de Broglie wavelength of a nitrogen molecule in air at 300 K? Assume that the molecule is moving with the root-mean square speed of molecules at this temperature. (Atomic mass of nitrogen = 14.0076 u)
Obtain the de Broglie wavelength associated with thermal neutrons at room temperature (27°C). Hence explain why a fast neutron beam needs to be thermalised with the environment before it can be used for neutron diffraction experiments.
Compute the typical de Broglie wavelength of an electron in a metal at 27°C and compare it with the mean separation between two electrons in a metal which is given to be about 2 × 10−10 m.
An electron is moving with an initial velocity `v = v_0hati` and is in a magnetic field `B = B_0hatj`. Then it’s de Broglie wavelength ______.
Assuming an electron is confined to a 1 nm wide region, find the uncertainty in momentum using Heisenberg Uncertainty principle (∆x∆p ≃ h). You can assume the uncertainty in position ∆x as 1 nm. Assuming p ≃ ∆p, find the energy of the electron in electron volts.
Two particles A and B of de Broglie wavelengths λ1 and λ2 combine to form a particle C. The process conserves momentum. Find the de Broglie wavelength of the particle C. (The motion is one dimensional).
Two particles move at a right angle to each other. Their de-Broglie wavelengths are λ1 and λ2 respectively. The particles suffer a perfectly inelastic collision. The de-Broglie wavelength λ, of the final particle, is given by ______.
