Advertisements
Advertisements
प्रश्न
A particle performing linear S.H.M. of period 2π seconds about the mean position O is observed to have a speed of `"b" sqrt3` m/s, when at a distance b (metre) from O. If the particle is moving away from O at that instant, find the time required by the particle, to travel a further distance b.
उत्तर
Data:
T = 2πs, v = `"b" sqrt3` m/s at x = b
∴ ω = `(2pi)/"T" = (2pi)/(2pi)` = 1 rad/s
v = `ω sqrt("A"^2 - "x"^2)`
∴ At x = b,
`"b" sqrt3 = (1) sqrt("A"^2 - "b"^2)`
∴ 3b2 = A2 − b2
∴ A = 2b
∴ Assuming the particle starts from the mean position, its displacement is given by x = A sin ωt = 2b sin t
If the particle is at x = b at t = t1,
b = 2b sint1
∴ t1 = sin−1 `1/2` = `pi/6`s
Also, with period T = 2πs, on travelling a further distance b the particle will reach the positive extremity at time t2 = `π/2`s.
∴ The time taken to travel a further distance b from x = b is
t2 − t1 = `pi/2 - pi/6`
= `(3pi - pi)/6`
= `(2pi)/6`
= `pi/3`s
संबंधित प्रश्न
Obtain the expression for the period of a magnet vibrating in a uniform magnetic field and performing S.H.M.
A wooden block of mass m is kept on a piston that can perform vertical vibrations of adjustable frequency and amplitude. During vibrations, we don’t want the block to leave the contact with the piston. How much maximum frequency is possible if the amplitude of vibrations is restricted to 25 cm? In this case, how much is the energy per unit mass of the block? (g ≈ π2 ≈ 10 m/s-2)
The period of oscillation of the simple pendulum increases by 20 %, when its length is increased by 44 cm. find its initial length.
What is meant by periodic motion? Give any two examples, for periodic motion.
What is meant by non-periodic motion? Give any two examples, for non-periodic motion.
What is meant by the force constant of a spring?
A particle performs simple harmonic motion with period of 3s. The time taken by It to cover a distance equal to half the amplitude from mean position is [sin 30° = 0.5]
A block of mass m attached to one end of the vertical spring produces extension x. If the block is pulled and released, the periodic time of oscillation is
A body of mass 64 g is made to oscillate turn by turn on two different springs A and B. Spring A and B has force constant 4 `"N"/"m"` and `16 "N"/"m"` respectively. If T1 and T2 are period of m oscillations of springs A and B respectively, then `("T"_1 + "T"_2)/("T"_1 - "T"_2)` will be ______.
The displacement of the particle executing linear S.H.M. is x = 0.25 Sill ( 11 l + 0.5) m. The period of S.H.M. is ______.
(`pi = 22/7` )
The ratio of frequencies of oscillations of two simple pendulums is 3: 4 then their lengths are in the ratio ______.
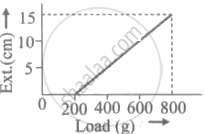
The pointer reading v/s load graph for a spring balance is as given in the figure. The spring constant is ______.
A particle starting from mean position oscillates simple harmonically with period 4 s. After what time will its kinetic energy be 75% of the total energy?
`( cos 30° = sqrt(3/2))`
The path length of oscillation of simple pendulum of length 1 meter is 16 cm. Its maximum velocity is ______. (g = π2 m/s2)
In an oscillator, for sustained oscillations, Barkhausen criterion is Aβ equal to ______.
(A = voltage gain without feedback and β feedback factor)
A block of mass 40 grams is suspended from an ideal spring and set into vertical oscillations. Find the mass to be added on the spring such that the period of oscillation increases by 25%.
Define the term oscillation.
