Advertisements
Advertisements
प्रश्न
A point charge q is at a distance of d/2 directly above the centre of a square of side d, as shown the figure. Use Gauss' law to obtain the expression for the electric flux through the square.
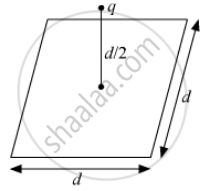
उत्तर
If we imagine a cube of side d, then this point charge q will be at the centre of the cube.
Now, the total electric flux due to this charge will pass evenly through the six faces of the cube.
So, the electric flux through one face will be equal to 1/6 of the total electric flux due to this charge.
Now, the total electric flux generated by the charge will be given by Gauss's law as :
`triangle phi = vecE.vec(triangleS)` = q/6∈0
So, the electric flux through the square = q/6∈∘">∈∘
APPEARS IN
संबंधित प्रश्न
Explain why, for a charge configuration, the equipotential surface through a point is normal to the electric field at that point
"For any charge configuration, equipotential surface through a point is normal to the electric field." Justify.
A point charge of 2.0 μC is at the centre of a cubic Gaussian surface 9.0 cm on edge. What is the net electric flux through the surface?
If the point charge is now moved to a distance 'd' from the centre of the square and the side of the square is doubled, explain how the electric flux will be affected.
Use Gauss' law to derive the expression for the electric field `(vecE)` due to a straight uniformly charged infinite line of charge density λ C/m.
Find the work done in bringing a charge q from perpendicular distance r1 to r2 (r2 > r1)
Which statement is true for Gauss law -
A spherical ball contracts in volume by 0.02% when subjected to a pressure of 100 atmosphere. Assuming one atmosphere = 105 Nm−2, the bulk modulus of the material of the ball is:
A solid metal sphere of radius R having charge q is enclosed inside the concentric spherical shell of inner radius a and outer radius b as shown in the figure. The approximate variation of the electric field `vecE` as a function of distance r from centre O is given by ______.

Draw a graph of kinetic energy as a function of linear charge density λ.
